题目内容
在一元二次方程ax2+bx+c=0(a≠0)中,有一根为0,则c= ;若a+b+c=0,则方程的一根为 ;若两根互为相反数,则b= .
考点:一元二次方程的解,根与系数的关系
专题:计算题
分析:根据一元二次方程的解把x=0代入原方程可求出对应的c的值;由于把x=1入原方程得到a+b+c=0,则可判断方程的一根为1;根据根与系数的关系当b=0时,
两根互为相反数.
两根互为相反数.
解答:解:把x=0代入ax2+bx+c=0得c=0
把x=1入ax2+bx+c=0得a+b+c=0,则a+b+c=0,方程的一根为1;
若两根互为相反数,则-
=0,所以b=0.
故答案为0,1,0.
把x=1入ax2+bx+c=0得a+b+c=0,则a+b+c=0,方程的一根为1;
若两根互为相反数,则-
| b |
| a |
故答案为0,1,0.
点评:本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.又因为只含有一个未知数的方程的解也叫做这个方程的根,所以一元二次方程的解也称为一元二次方程的根.也考查了根与系数的关系.

练习册系列答案
相关题目
下列式子:①
;②
;③
;④
.其中是二次根式的有( )
|
| -5 |
| 3 | 8 |
| (-2)2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
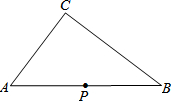 如图,P是Rt△ABC斜边AB上一点(A、B两点除外),过点P作一直线,使截得的三角形与Rt△ABC相似,这样的直线可以作( )
如图,P是Rt△ABC斜边AB上一点(A、B两点除外),过点P作一直线,使截得的三角形与Rt△ABC相似,这样的直线可以作( )| A、1条 | B、2条 | C、3条 | D、4条 |
 如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=6cm,CD⊥AB于D,以C为圆心,CD为半径画弧,交BC于E,则图中阴影部分的面积为
如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=6cm,CD⊥AB于D,以C为圆心,CD为半径画弧,交BC于E,则图中阴影部分的面积为 如图,∠1=∠2=30°,∠3=∠4,∠A=80°,则∠CDE=
如图,∠1=∠2=30°,∠3=∠4,∠A=80°,则∠CDE=