题目内容
观察下面有※组成的图案和算式：1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
请猜想1+3+5+7+9+…+（2n+1）=
考点：规律型：数字的变化类
专题：
分析：根据观察，可发现从1开始几个连续的奇数的和，就是几的平方．
解答：解：1+3+5+7+9+…+（2n+1）=（n+1）2．
故答案为：（n+1）2．
故答案为：（n+1）2．
点评：本题考查了数字的变化类，求连续（n+1）个奇数的和是解题关键．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
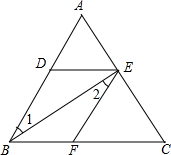根据题意结合图形填空：
已知，如图，在四边形ABCD中，E、F、G、H分别是AB、CD、AC、BD的中点，