题目内容
若抛物线y=x2-2x+c与y轴的交点为（0，-3），则下列说法不正确的是（ ）
| A、抛物线开口向上 |
| B、抛物线与x轴的交点为（-1，0），（3，0） |
| C、当x=1时，y的最大值为-4 |
| D、抛物线的对称轴是直线x=1 |
考点：抛物线与x轴的交点
专题：
分析：把（0，-3）代入抛物线解析式求c的值，然后再求出顶点坐标、与x轴的交点坐标．
解答：解：把（0，-3）代入y=x2-2x+c中得c=-3，
抛物线为y=x2-2x-3=（x-1）2-4=（x+1）（x-3），
所以抛物线开口向上，对称轴是x=1，
当x=1时，y的最小值为-4，
与x轴的交点为（-1，0），（3，0）；C错误．
故选：C．
抛物线为y=x2-2x-3=（x-1）2-4=（x+1）（x-3），
所以抛物线开口向上，对称轴是x=1，
当x=1时，y的最小值为-4，
与x轴的交点为（-1，0），（3，0）；C错误．
故选：C．
点评：本题主要考查了抛物线与x轴的交点，解题的关键是熟练掌握抛物线的性质及a，b，c的相关运用．
练习册系列答案
相关题目
若a-b=2，a-c=1，则（2a-b-c）2+（c-b）2的值为（ ）
| A、10 | B、11 | C、9 | D、12 |
如图，△OAB绕点O逆时针旋转85°到△OCD的位置，已知∠A=80°，∠D=60°则∠AOD等于（ ）| A、55° | B、45° |
| C、40° | D、35° |
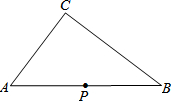如图，P是Rt△ABC斜边AB上一点（A、B两点除外），过点P作一直线，使截得的三角形与Rt△ABC相似，这样的直线可以作（ ）| A、1条 | B、2条 | C、3条 | D、4条 |
在分式
，
，
，
中，最简分式有（ ）
| b |
| 8a |
| a-b |
| a+b |
| x-y |
| x2+y2 |
| x-y |
| x2-y2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
如果把分式
中的a、b都扩大5倍，那么分式的值一定（ ）
| 5ab |
| a-2b |
| A、扩大5倍 | B、扩大25倍 |
| C、不变 | D、缩小5倍 |
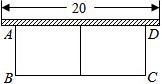如图，有长为30m的篱笆，一面得用墙（墙的最大可用长度为20m），围成中间隔有一道篱笆（平行于AB）的矩形花圃．