题目内容
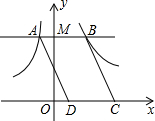 如图,过y轴上一个动点M作x轴的平行线,交双曲线y=-
如图,过y轴上一个动点M作x轴的平行线,交双曲线y=-| 4 |
| x |
| 10 |
| x |
| A、7 | B、10 | C、14 | D、28 |
考点:反比例函数系数k的几何意义
专题:
分析:设出M点的坐标,可得出过M与x轴平行的直线方程为y=m,将y=m代入反比例函数y=-
中,求出对应的x的值,即为A的横坐标,将y=m代入反比例函数y=
中,求出对应的x的值,即为B的横坐标,用B的横坐标减去A的横坐标求出AB的长,根据DC=AB,且DC与AB平行,得到四边形ABCD为平行四边形,过B作BN垂直于x轴,平行四边形的底边为DC,DC边上的高为BN,由B的纵坐标为m,得到BN=m,再由求出的AB的长,得到DC的长,利用平行四边形的面积等于底乘以高可得出平行四边形ABCD的面积.
| 4 |
| x |
| 10 |
| x |
解答:解:设M的坐标为(0,m)(m>0),则直线AB的方程为:y=m,
将y=m代入y=-
中得:x=-
,∴A(-
,m),
将y=m代入y=
中得:x=
,∴B(
,m),
∴DC=AB=
-(-
)=
,
过B作BN⊥x轴,则有BN=m,
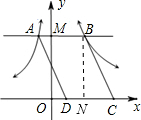
则平行四边形ABCD的面积S=DC•BN=
•m=14.
故选C.
将y=m代入y=-
| 4 |
| x |
| 4 |
| m |
| 4 |
| m |
将y=m代入y=
| 10 |
| x |
| 10 |
| m |
| 10 |
| m |
∴DC=AB=
| 10 |
| m |
| 4 |
| m |
| 14 |
| m |
过B作BN⊥x轴,则有BN=m,

则平行四边形ABCD的面积S=DC•BN=
| 14 |
| m |
故选C.
点评:此题属于反比例函数综合题,涉及的知识有:平面直角坐标系与坐标,反比例函数的性质,平行四边形的面积求法,以及一次函数与反比例函数的交点,利用了数形结合的思想,其中设出M的坐标,表示出过M与x轴平行的直线方程是本题的突破点.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
下列式子:①
;②
;③
;④
.其中是二次根式的有( )
|
| -5 |
| 3 | 8 |
| (-2)2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
第九届中国国际园林博览会正在北京丰台举行,预计参观人数17000000人次,是国内园林花卉界最高层次的盛会,将17000000用科学记数法表示应为( )
| A、0.17×108 |
| B、17×106 |
| C、1.7×107 |
| D、1.7×108 |
若a-b=2,a-c=1,则(2a-b-c)2+(c-b)2的值为( )
| A、10 | B、11 | C、9 | D、12 |
 如图,△OAB绕点O逆时针旋转85°到△OCD的位置,已知∠A=80°,∠D=60°则∠AOD等于( )
如图,△OAB绕点O逆时针旋转85°到△OCD的位置,已知∠A=80°,∠D=60°则∠AOD等于( )| A、55° | B、45° |
| C、40° | D、35° |
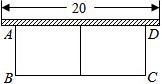 如图,有长为30m的篱笆,一面得用墙(墙的最大可用长度为20m),围成中间隔有一道篱笆(平行于AB)的矩形花圃.
如图,有长为30m的篱笆,一面得用墙(墙的最大可用长度为20m),围成中间隔有一道篱笆(平行于AB)的矩形花圃.