题目内容
5.已知关于x的一元二次方程x2+mx+n=0的两根分别是一个直角三角形两锐角的余弦值,且-n=$\frac{m-1}{5}$,求m,n的值.分析 设直角三角形的两锐角分别为α,β,根据根与系数的关系表示出两根之和与两根之积,利用同角三角函数间的基本关系变形,再利用完全平方公式化简,将-n=$\frac{m-1}{5}$代入,得到关于m的方程,求出方程的解即可得到m的值,进而得出n.
解答 解:设直角三角形的两锐角分别为α,β,
根据题意得:方程x2+mx+n=0的两根为cosα与cosβ(sinα=cosβ),
∴cosα+cosβ=cosα+sinα=-m,cosαsinα=n>0,
又sin2α+cos2α=1,
∴(cosα+sinα)2-2sinαcosα=m2-2n=1,
∵-n=$\frac{m-1}{5}$,
∴m2-2(-$\frac{m-1}{5}$)=1,
整理得:5m2+2m-7=0,
解得:m=1或-$\frac{7}{5}$,
当m=1时,-n=0,不合题意舍去;
当m=-$\frac{7}{5}$时,-n=$\frac{-12}{25}$,n=$\frac{12}{25}$,符合题意.
故m=-$\frac{7}{5}$,n=$\frac{12}{25}$.
点评 此题考查了一元二次方程根与系数的关系,以及互余两角三角函数的关系,熟练掌握根与系数的关系是解本题的关键.

练习册系列答案
相关题目
 如图,四边形ABCD∽四边形A′B′C′D′,求边x、y的长度和角α的大小.
如图,四边形ABCD∽四边形A′B′C′D′,求边x、y的长度和角α的大小.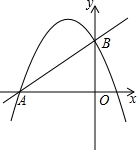 如图,在平面直角坐标系中,直线AB和抛物线交于点A(-4,0),B(0,4),且抛物线的对称轴为直线x=-1.
如图,在平面直角坐标系中,直线AB和抛物线交于点A(-4,0),B(0,4),且抛物线的对称轴为直线x=-1. 如图所示,若要使AB∥ED,则∠ABC,∠C,∠D应满足什么条件?证明你的结论.
如图所示,若要使AB∥ED,则∠ABC,∠C,∠D应满足什么条件?证明你的结论. 如图,在△ABC中,∠A=45°,直线l与边AB、AC分别交于点M、N,则∠1+∠2的度数是225°.
如图,在△ABC中,∠A=45°,直线l与边AB、AC分别交于点M、N,则∠1+∠2的度数是225°.