题目内容
15.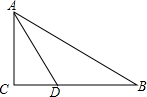 如图,在Rt△ABC中,∠C=90°,AC=4,∠A的平分线AD=$\frac{8\sqrt{3}}{3}$,求∠B的度数及边BC、AB的长.
如图,在Rt△ABC中,∠C=90°,AC=4,∠A的平分线AD=$\frac{8\sqrt{3}}{3}$,求∠B的度数及边BC、AB的长.
分析 在RT△ACD中利用cos∠CAD=$\frac{AC}{AD}$=$\frac{\sqrt{3}}{2}$,求出∠ACD,再求出∠CAB,最后在RT△ABC根据30度性质求解.
解答 解:在RT△ACD中,∵∠C=90°,AC=4,AD=$\frac{8\sqrt{3}}{3}$,
∴cos∠CAD=$\frac{AC}{AD}$=$\frac{\sqrt{3}}{2}$,
∴∠CAD=30°,
∵AD平分∠CAB,∴∠CAB=2∠CAD=60°,
∴∠B=90°-∠CAB=30°,
∴AB=2AC=8,BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$.
点评 本题考查三角函数的定义、勾股定理、角平分线的定义等知识,正确运用三角函数的定义是解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
6.将抛物线y=2x2向左平移1个单位,再向上平移3个单位得到的抛物线表达式是( )
| A. | y=2(x-1)2-3 | B. | y=2(x+1)2+3 | C. | y=2(x-1)2+3 | D. | y=2(x+1)2-3 5. |
3.-$\frac{2}{3}$的倒数是( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | $\frac{1}{3}$ |
10.公司9月份利润为100万元,要使11月份的利润达到144万元,则平均每月增长的百分率为( )
| A. | 10% | B. | 20% | C. | 22% | D. | 25% |
 等腰△ABC的底边上高AD与底角平分线CE交于点P,EF⊥AD,F为垂足,若线段EB=4,则线段EF=2.
等腰△ABC的底边上高AD与底角平分线CE交于点P,EF⊥AD,F为垂足,若线段EB=4,则线段EF=2.