题目内容
8.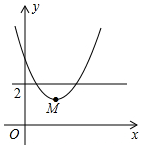 如图,平面直角坐标系中,点M是直线y=2与x轴之间的一个动点,且点M是抛物线y=$\frac{1}{2}{x^2}$+bx+c的顶点,则抛物线y=$\frac{1}{2}{x^2}$+bx+c与直线y=1交点的个数是( )
如图,平面直角坐标系中,点M是直线y=2与x轴之间的一个动点,且点M是抛物线y=$\frac{1}{2}{x^2}$+bx+c的顶点,则抛物线y=$\frac{1}{2}{x^2}$+bx+c与直线y=1交点的个数是( )| A. | 0个或1个 | B. | 0个或2个 | C. | 1个或2个 | D. | 0个、1个或2个 |
分析 令y=$\frac{1}{2}$x2+bx+c,y=1,要求方程$\frac{1}{2}$x2+bx+c=1的解的个数,只需求抛物线y=$\frac{1}{2}$x2+bx+c与直线y=1有没有交点即可.
解答 解:由抛物线y=$\frac{1}{2}$x2+bx+c的图象可知,该抛物线与x轴没有交点,
即:△<0,
则:b2-4c<0,
又点M是直线y=2与x轴之间的一个动点,点M的坐标为:(-b,$\frac{2c-{b}^{2}}{2}$),
所以,0<$\frac{2c-{b}^{2}}{2}$<2,即:-4<b2-2c<0,
∴:-2<b2-2c+2<2,
联立抛物线解析式y=$\frac{1}{2}$x2+bx+c和直线y=1,
则要求方程$\frac{1}{2}$x2+bx+c=1的解得个数,
又因为,△=b2-4×$\frac{1}{2}$(c-1)=b2-2(c-1)=b2-2c+2,
所以,-2<b2-2c+2<2,
即:①当-2<b2-2c+2<0时,抛物线y=$\frac{1}{2}$x2+bx+c与直线y=1没有交点;
②b2-2c+2=0时,抛物线y=$\frac{1}{2}$x2+bx+c与直线y=1有一个交点;
③0<b2-2c+2<2时,抛物线y=$\frac{1}{2}$x2+bx+c与直线y=1有两个交点.
故选:D.
点评 本题考查了抛物线与x轴的交点问题,解题的关键是理解二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点与一元二次方程ax2+bx+c=0根之间的关系.

 阅读快车系列答案
阅读快车系列答案| A. | 2a•3a=6a | B. | (2a2)3=8a6 | C. | a8÷a4=a2 | D. | (a+b)2=a2+b2 |
| A. | 3 | B. | -1 | C. | 3或-1 | D. | -3或1 |
| 时间x(天) | 每台空调的成本P(元) |
| 0<x≤5 | P=400 |
| 5<x≤12 | P=40x+200 |
请解答下列问题:
(1)设厂家的日销售利润为W元,求W(元)与时间x(天)的函数关系式;
(2)确定该厂哪一天获得最大利润,最大利润是多少?
(3)设厂家在第一个产销期,获得最大利润时的成本为P1,日生产量为y1.
现计划从第13天开始,按每台成本P1元,每台生产y1台进行生产并完全售出,但由于机器损耗等原因,实际平均每台空调的成本比统计增加了a%,使得厂家10天的销售利润与原计划的8天的销售利润持平,求a的值.
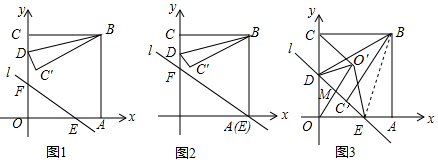
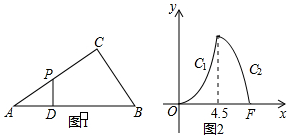 如图1,在Rt△ABC中,∠C=Rt∠,∠A=30°,D为AB上一个动点,过点D作DP⊥AB交折线A-C-B于点P,设AD的长为x,△APD的面积为y,y关于x的函数图象由C1,C2两段组成,如图2所示.
如图1,在Rt△ABC中,∠C=Rt∠,∠A=30°,D为AB上一个动点,过点D作DP⊥AB交折线A-C-B于点P,设AD的长为x,△APD的面积为y,y关于x的函数图象由C1,C2两段组成,如图2所示.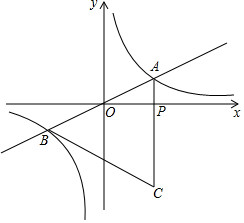 如图,直线y=kx与双曲线y=$\frac{\sqrt{3}}{x}$在一三象限分别交于A、B两点,等边△ABC的边AC交x轴于P点.
如图,直线y=kx与双曲线y=$\frac{\sqrt{3}}{x}$在一三象限分别交于A、B两点,等边△ABC的边AC交x轴于P点.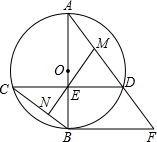 如图,AB为⊙O直径,且弦CD⊥AB于点E,过点B作⊙O的切线与AD的延长线交于点F.
如图,AB为⊙O直径,且弦CD⊥AB于点E,过点B作⊙O的切线与AD的延长线交于点F.