题目内容
1.用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干图按:
设每个图案汇总黑砖的块数为n.
(1)如图1,当黑砖n=1时,白砖有6块;如图2,当黑砖n=2时,白砖有10块;那么,当n=4时,白砖有18块.
(2)第n个图案中,白色地砖共(4n+2)块.
分析 (1)第1个图里有白色地砖6+4(1-1)=6;第2个图里有白色地砖6+4(2-1)=10;第4个图里有白色地砖6+4(4-1)=18;…;
(2)由(1)得出第n个图里有白色地砖6+4(n-1)=4n+2.
解答 解:∵每个图形都比其前一个图形多4个白色地砖,
∴可得规律为:第n个图形中有白色地砖6+4(n-1)=(4n+2)块;
(1)第2个图里有白色地砖6+4(2-1)=10块;第4个图里有白色地砖6+4(4-1)=18块;
(2)第n个图里有白色地砖6+4(n-1)=(4n+2)块;
故答案为:10,18,(4n+2).
点评 此题考查图形的变化规律,重点考查了通过特例分析从而归纳总结出一般结论的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.在平行四边形ABCD中,∠A+∠C=100°,则∠D=( )
| A. | 130° | B. | 120° | C. | 70° | D. | 80° |
11.如果一元二次方程x2-ax+3=0经配方后,得(x-2)2=1,则a的值为( )
| A. | 1 | B. | -1 | C. | 4 | D. | -4 |
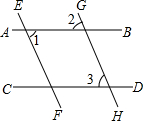 完成下面推理过程
完成下面推理过程
 已知二次函数y=-x2-2x+m的部分图象如图所示,则关于x的一元二次方程x2+2x=m的解为x1=-3,x2=1.
已知二次函数y=-x2-2x+m的部分图象如图所示,则关于x的一元二次方程x2+2x=m的解为x1=-3,x2=1. 如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(-1,3),B(-4,0),C(0,0)
如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(-1,3),B(-4,0),C(0,0)