题目内容
13. 如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(-1,3),B(-4,0),C(0,0)
如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(-1,3),B(-4,0),C(0,0)(1)画出将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△A1B1C1,并直接写出坐标:A1(4,4),B1(1,1),C1(5,1);
(2)画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O,并直接写出坐标:A2(3,1),B2(0,4)
(3)在x轴上存在一点P,满足点P到A1与点A2距离之和最小,请求出点P的坐标.
分析 (1)分别将点A、B、C向上平移1个单位,再向右平移5个单位,然后顺次连接得到△A1B1C1,然后写出A1,B1,C1的坐标即可;
(2)根据网格结构找出点A、B、C以点O为旋转中心顺时针旋转90°后的对应点,然后顺次连接得到△A2B2O,然后写出A2,B2的坐标即可;
(3)首先作A1点关于x轴的对称点A3,再连接A2A3与x轴的交点即为点P.利用待定系数法求出直线A2A3的解析式,将y=0代入,计算出x的值,即可得到点P的坐标.
解答 解:(1)如图所示,△A1B1C1为所求作的三角形.
A1(4,4),B1(1,1),C1(5,1).
故答案为4,4,1,1,5,1;
(2)如图所示,△A2B2O为所求作的三角形.
A2(3,1),B2(0,4).
故答案为3,1,0,4;
(3)作A1点关于x轴的对称点A3,连接A2A3与x轴的交点即为点P..
∵A2坐标为(3,1),A3坐标为(4,-4),
∴A2A3所在直线的解析式为:y=-5x+16,
令y=0,则x=$\frac{16}{5}$,
∴P点的坐标($\frac{16}{5}$,0).
点评 本题考查了利用旋转和平移变换作图,轴对称的性质,利用待定系数法求直线的解析式,熟练掌握网格结构准确找出对应点的位置作出所需图形是解题的关键.

练习册系列答案
相关题目
8.在平面直角坐标系中,把点P(-2,3)向右平移5个单位得到点P1,再将点P1绕原点旋转90°得到点P2,则点P2的坐标是( )
| A. | (3,-3) | B. | (-3,3) | C. | (3,3)或(-3,-3) | D. | (3,-3)或(-3,3) |
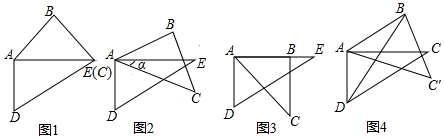
3. 如图所示,△ABC≌△ADC,∠ABC=70°,则∠ADC的度数是( )
如图所示,△ABC≌△ADC,∠ABC=70°,则∠ADC的度数是( )
 如图所示,△ABC≌△ADC,∠ABC=70°,则∠ADC的度数是( )
如图所示,△ABC≌△ADC,∠ABC=70°,则∠ADC的度数是( )| A. | 70° | B. | 45° | C. | 30° | D. | 35° |

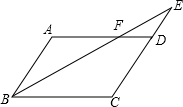 如图,在平行四边形ABCD中,E为CD延长线上的一点,BE交AD于F,DE=$\frac{1}{2}$CD=$\frac{1}{2}$AB
如图,在平行四边形ABCD中,E为CD延长线上的一点,BE交AD于F,DE=$\frac{1}{2}$CD=$\frac{1}{2}$AB