题目内容
9.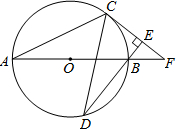 如图,AB为⊙O的直径,C,D为⊙O上不同于A,B的两点,过点C作⊙O的切线CF交直线AB于点F,直线DB⊥CF于点E.
如图,AB为⊙O的直径,C,D为⊙O上不同于A,B的两点,过点C作⊙O的切线CF交直线AB于点F,直线DB⊥CF于点E.(1)求证:∠ABD=2∠CAB;
(2)若BF=5,sin∠F=$\frac{3}{5}$,求BD的长.
分析 (1)连接OC,根据等腰三角形性质和外角的性质得出∠2=2∠CAB,根据切线的性质得出OC⊥CF,即可证得OC∥DB,根据平行线的性质得出∠ABD=∠2,即可证得∠ABD=2∠CAB;
(2)连接AD,根据圆周角定理得出AD⊥DE,即可证得AD∥CF,根据平行线的性质得出∠3=∠F,从而证得△FBE∽△FOC,根据三角形相似的性质求得半径,然后通过解直角三角形即可求得BD的长.
解答 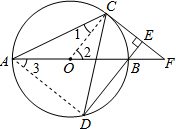 (1)证明:连接OC,
(1)证明:连接OC,
∵OA=OC,
∴∠CAB=∠1,
∴∠2=∠CAB+∠1=2∠CAB,
∵CF切⊙O于C,OC是⊙O的半径,
∴OC⊥CF,
∵DB⊥CF,
∴OC∥DB,
∴∠ABD=∠2,
∴∠ABD=2∠CAB;
(2)解:连接AD,
∵AB为⊙O的直径,
∴∠ADB=90°,即AD⊥DE,
∵DE⊥CF,
∴AD∥CF,
∴∠3=∠F,
在RT△BEF中,∵∠BEF=90°,BF=5,sin∠F=$\frac{3}{5}$,
∴BE=BF•sin∠F=5×$\frac{3}{5}$=3,
∵OC∥BE,
∴△FBE∽△FOC,
∴$\frac{FB}{FO}$=$\frac{BE}{OC}$,
设⊙O的半径为r,则$\frac{5}{5+r}$=$\frac{3}{r}$,
解得r=$\frac{15}{2}$,
在RT△ABD中,∠ADB=90°,AB=2r=15,sin∠3=sin∠F=$\frac{3}{5}$,
∴BD=AB•sin∠3=15×$\frac{3}{5}$=9.
点评 本题考查了切线的性质,平行线的判定和性质,三角形相似的判定和性质,解直角三角形等,作出辅助线是解题的关键.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
20.2015年9月3日,纪念中国人民抗日战争暨世界反法西斯战争胜利70周年大会在北京隆重举行.在此次活动中,共有11个徒步方队,27个装备方队12 000名官兵通过天安门广场接受党和人民的检阅.将数字12 000用科学记数法表示为( )
| A. | 12×103 | B. | 1.2×104 | C. | 1.2×105 | D. | 0.12×105 |
4.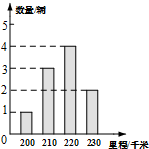 为了解某种电动汽车一次充电后行驶的里程数,抽检了10辆车,统计结果如图所示,则在一次充电后行驶的里程数这组数据中,众数和中位数分别是( )
为了解某种电动汽车一次充电后行驶的里程数,抽检了10辆车,统计结果如图所示,则在一次充电后行驶的里程数这组数据中,众数和中位数分别是( )
 为了解某种电动汽车一次充电后行驶的里程数,抽检了10辆车,统计结果如图所示,则在一次充电后行驶的里程数这组数据中,众数和中位数分别是( )
为了解某种电动汽车一次充电后行驶的里程数,抽检了10辆车,统计结果如图所示,则在一次充电后行驶的里程数这组数据中,众数和中位数分别是( )| A. | 220,220 | B. | 220,210 | C. | 200,220 | D. | 230,210 |
1.下列命题中:
①立方根等于它本身的数有-1,0,1;
②负数没有立方根;
③$\root{3}{6}$=2;
④任何正数都有两个立方根,且它们互为相反数;
⑤平方根等于它本身的数有0和1.
正确的有( )
①立方根等于它本身的数有-1,0,1;
②负数没有立方根;
③$\root{3}{6}$=2;
④任何正数都有两个立方根,且它们互为相反数;
⑤平方根等于它本身的数有0和1.
正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.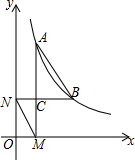 如图,点A、B都在双曲线y=$\frac{k}{x}$的图象上,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN相交于点C,若AB=2MN,点M(1,0),ON=$\frac{3}{2}$,则k的值是( )
如图,点A、B都在双曲线y=$\frac{k}{x}$的图象上,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN相交于点C,若AB=2MN,点M(1,0),ON=$\frac{3}{2}$,则k的值是( )
 如图,点A、B都在双曲线y=$\frac{k}{x}$的图象上,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN相交于点C,若AB=2MN,点M(1,0),ON=$\frac{3}{2}$,则k的值是( )
如图,点A、B都在双曲线y=$\frac{k}{x}$的图象上,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN相交于点C,若AB=2MN,点M(1,0),ON=$\frac{3}{2}$,则k的值是( )| A. | $\frac{3}{2}$ | B. | 2 | C. | 3 | D. | $\frac{9}{2}$ |