题目内容
8. 如图,四边形ABCD是平行四边形,AD=30cm,AB=20cm,∠D=60°,E、F分别为AB和CD边上的两个动点,E从A向B运动,F从D向C运动,若点E的速度是1cm/秒,点F的速度是2cm/秒.
如图,四边形ABCD是平行四边形,AD=30cm,AB=20cm,∠D=60°,E、F分别为AB和CD边上的两个动点,E从A向B运动,F从D向C运动,若点E的速度是1cm/秒,点F的速度是2cm/秒.(Ⅰ)当点E和点F同时出发时,出发后几秒时四边形AECF是平行四边形.
(Ⅱ)在点E和点F同时出发的情况下,四边形AECF有没有成为矩形的可能?若认为能,请求出发后的时间;或认为不能,请说明理由.
分析 (1)由平行四边形的性质得出AB∥CD,若四边形AECF是平行四边形,则AE=CF,得出方程t=20-2t,解方程即可;解得:t=$\frac{20}{3}$;
(2)由平行四边形的性质得出∠BAD=120°,若四边形AECF是矩形,则∠EAF=90°,求出∠DAF=30°,由含30°角的直角三角形的性质得出DF=$\frac{1}{2}$AD=15cm=2t,求出t=$\frac{15}{2}$,CF=CD-DF=5,此时AE=7.5≠5,得出四边形AECF不是平行四边形,产生矛盾,即可得出结论.
解答 解:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,
若四边形AECF是平行四边形,则AE=CF,
即t=20-2t,
解得:t=$\frac{20}{3}$;
即当点E和点F同时出发时,出发后$\frac{20}{3}$秒时四边形AECF是平行四边形.
(2)在点E和点F同时出发的情况下,四边形AECF没有成为矩形的可能;理由如下:
∵四边形ABCD是平行四边形,∠D=60°,
∴∠BAD=120°,
若四边形AECF是矩形,则∠EAF=90°,
∴∠DAF=30°,
∴DF=$\frac{1}{2}$AD=15cm=2t,
∴t=$\frac{15}{2}$,CF=CD-DF=5,
此时AE=7.5≠5,
∴四边形AECF不是平行四边形,
∴在点E和点F同时出发的情况下,四边形AECF没有成为矩形的可能.
点评 本题考查了平行四边形的判定与性质、矩形的判定与性质;熟练掌握平行四边形的判定与性质是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.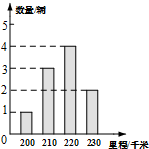 为了解某种电动汽车一次充电后行驶的里程数,抽检了10辆车,统计结果如图所示,则在一次充电后行驶的里程数这组数据中,众数和中位数分别是( )
为了解某种电动汽车一次充电后行驶的里程数,抽检了10辆车,统计结果如图所示,则在一次充电后行驶的里程数这组数据中,众数和中位数分别是( )
 为了解某种电动汽车一次充电后行驶的里程数,抽检了10辆车,统计结果如图所示,则在一次充电后行驶的里程数这组数据中,众数和中位数分别是( )
为了解某种电动汽车一次充电后行驶的里程数,抽检了10辆车,统计结果如图所示,则在一次充电后行驶的里程数这组数据中,众数和中位数分别是( )| A. | 220,220 | B. | 220,210 | C. | 200,220 | D. | 230,210 |
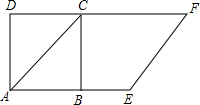 如图,以正方形ABCD的对角线AC为一边,延长AB到E,使AE=AC,以AE为一边作菱形AEFC,若菱形的面积为9$\sqrt{2}$cm2,则正方形ABCD的面积为9.
如图,以正方形ABCD的对角线AC为一边,延长AB到E,使AE=AC,以AE为一边作菱形AEFC,若菱形的面积为9$\sqrt{2}$cm2,则正方形ABCD的面积为9.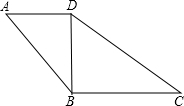 如图,在四边形ABCD中,AD∥BC,∠A=∠BDC.
如图,在四边形ABCD中,AD∥BC,∠A=∠BDC.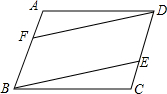 如图,在?ABCD中,点E、F分别在DC、AB上,DC=3CE,BF=2AF,求证:DF=BF,DF∥BF.
如图,在?ABCD中,点E、F分别在DC、AB上,DC=3CE,BF=2AF,求证:DF=BF,DF∥BF.