题目内容
12. 如图,长方形内有两个相邻的正方形,面积分别为2和4,则阴影部分的面积为( )
如图,长方形内有两个相邻的正方形,面积分别为2和4,则阴影部分的面积为( )| A. | $2\sqrt{2}-2$ | B. | $2\sqrt{2}+2$ | C. | 2 | D. | $1+\sqrt{2}$ |
分析 根据正方形的面积公式求得两个正方形的边长分别是$\sqrt{2}$,2,再根据阴影部分的面积等于矩形的面积减去两个正方形的面积进行计算.
解答 解:∵矩形内有两个相邻的正方形面积分别为4和2,
∴两个正方形的边长分别是$\sqrt{2}$,2,
∴阴影部分的面积=(2+$\sqrt{2}$)×2-2-4=2$\sqrt{2}$-2.
故选:A.
点评 本题考查了算术平方根,解决本题的关键是要能够由正方形的面积表示出正方形的边长,再进一步表示矩形的长.

练习册系列答案
相关题目
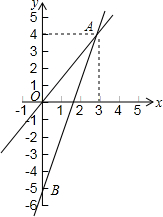 如图表示一个正比例函数与一个一次函数的图象,它们交于点A(4,3),一次函数的图象与y轴交于点B,且OA=OB.
如图表示一个正比例函数与一个一次函数的图象,它们交于点A(4,3),一次函数的图象与y轴交于点B,且OA=OB.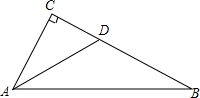 如图,在Rt△ABC中,∠C=90°,AD平分∠A,交边BC于点D,BD=2CD,求证:BC=$\sqrt{3}$•AC.
如图,在Rt△ABC中,∠C=90°,AD平分∠A,交边BC于点D,BD=2CD,求证:BC=$\sqrt{3}$•AC.