题目内容
14．已知θ为锐角，且$\frac{1}{x}$=1+sinθ，则|2x-1|+|2x-9|的值为（ ）| A． | 10 | B． | 8 | C． | 由θ的大小而定 | D． | 无法确定 |
分析 根据当θ为锐角时，0＜sinθ＜1，求出x的取值范围，根据绝对值的性质化简代数式即可．
解答 解：∵$\frac{1}{x}$=1+sinθ，
∴x=$\frac{1}{1+sinθ}$，
∵0＜sinθ＜1，
∴1＜1+sinθ＜2，
∴$\frac{1}{2}$＜x＜1，
则1＜2x＜2，
∴|2x-1|+|2x-9|=2x-1+9-2x=8，
故选：B．
点评 本题考查的是锐角三角函数的定义和性质，掌握当θ为锐角时，0＜sinθ＜1是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，在?ABCD中，AE⊥BC于E，AF⊥CD于F，∠BAD=120°，则∠EAF=60°．
2．解方程：$\frac{4}{4{x}^{2}-1}$-$\frac{2}{2x-1}$=0．x=（ ）
| A． | 1 | B． | $\frac{1}{2}$ | C． | 2 | D． | 无解 |
19．下列运算正确的是（ ）
| A． | |-6|=6 | B． | $（\frac{1}{2}）^{-1}=-2$ | C． | $\sqrt{16}=±4$ | D． | a2•a3=a6 |
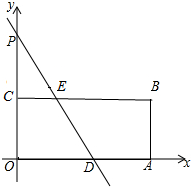在平面直角坐标系中，矩形OABC的两个顶点坐标分别为A（12，0），B（12，6），已知点P（0，12）．
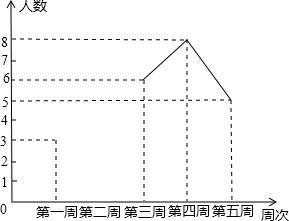为配合我校开展的“书香校园”活动，校团委对我校某班同学近五周的读书情况进行了调查，将当周每日都坚持课外阅读的同学评为“读书之星”并将“读书之星”的人数与周次制成了如下不完整的折线统计图：