题目内容
2．解方程：$\frac{4}{4{x}^{2}-1}$-$\frac{2}{2x-1}$=0．x=（ ）| A． | 1 | B． | $\frac{1}{2}$ | C． | 2 | D． | 无解 |
分析 分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．
解答 解：去分母得：4-2（2x+1）=0，
解得：x=$\frac{1}{2}$，
经检验x=$\frac{1}{2}$是增根，分式方程无解，
故选D
点评 此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．
练习册系列答案
相关题目
12．
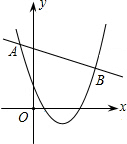已知二次函数${y_1}=a{x^2}+bx+c$（a≠0）与一次函数y2=kx+m（k≠0）的图象交于点A（-2，4），B（8，2），如图所示，则能使y1＞y2成立的x的取值范围是（ ）
已知二次函数${y_1}=a{x^2}+bx+c$（a≠0）与一次函数y2=kx+m（k≠0）的图象交于点A（-2，4），B（8，2），如图所示，则能使y1＞y2成立的x的取值范围是（ ）| A． | x＜-2 | B． | x＞8 | C． | -2＜x＜8 | D． | x＜-2或x＞8 |
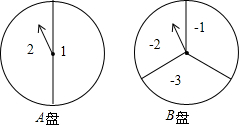如图有两个可自由转动的转盘，A转盘被平均分成2个相等的扇形区域，分别标注数字1和2；B转盘被平均分成3个相等的扇形区域，分别标注数字-1，-2，-3．分别转动这两个转盘，将A盘所得结果记为x，B盘所得结果记为y，这样就确定了点P的坐标（x，y）
14．已知θ为锐角，且$\frac{1}{x}$=1+sinθ，则|2x-1|+|2x-9|的值为（ ）
| A． | 10 | B． | 8 | C． | 由θ的大小而定 | D． | 无法确定 |
三角形的顶点坐标分别是A（2，2），B（4，2），C（6，4），试将△ABC缩小，使缩小后的△DEF与△ABC对应边的比为1：2．画出图形并写出各点的坐标．