题目内容
5.二次函数y=x2+a的图象过点(-3,4),则a=-5.分析 根据二次函数图象上点的坐标特征,把点(-3,4)代入解析式可得到关于a的方程,然后解关于a的方程即可.
解答 解:∵二次函数y=x2+a的图象过点(-3,4),
∴9+a=4,
∴a=-5.
故答案为-5.
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
15.我市嘉积镇组织20辆汽车装运完A、B、C三种荔枝共100吨到外地销售.按计划,20辆汽车都要装运,每辆汽车只能装运同一种荔枝,且必须装满.根据下表提供的信息,解答以下问题:
(1)设装运A种荔枝的车辆数为x,装运B种荔枝的车辆数为y,求y与x之间的函数关系式;
(2)若装运每种荔枝的车辆数都不少于4辆,则车辆的安排方案有几种,并写出具体方案;若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.
| 荔枝 品 种 | A | B | C |
| 每辆汽车运载量(吨) | 6 | 5 | 4 |
| 每吨荔枝获得(百元) | 12 | 16 | 10 |
(2)若装运每种荔枝的车辆数都不少于4辆,则车辆的安排方案有几种,并写出具体方案;若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.
14.已知θ为锐角,且$\frac{1}{x}$=1+sinθ,则|2x-1|+|2x-9|的值为( )
| A. | 10 | B. | 8 | C. | 由θ的大小而定 | D. | 无法确定 |
15.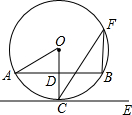 如图,AB是⊙O的弦,半径OC经过AB的中点D,CE∥AB,点F在⊙O上,连接CF,BF,下列结论中,不正确的是( )
如图,AB是⊙O的弦,半径OC经过AB的中点D,CE∥AB,点F在⊙O上,连接CF,BF,下列结论中,不正确的是( )
 如图,AB是⊙O的弦,半径OC经过AB的中点D,CE∥AB,点F在⊙O上,连接CF,BF,下列结论中,不正确的是( )
如图,AB是⊙O的弦,半径OC经过AB的中点D,CE∥AB,点F在⊙O上,连接CF,BF,下列结论中,不正确的是( )| A. | ∠F=$\frac{1}{2}∠AOC$ | B. | AB⊥BF | C. | CE是⊙O的切线 | D. | $\widehat{AC}=\widehat{BC}$ |
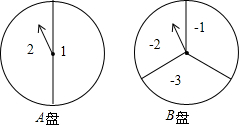 如图有两个可自由转动的转盘,A转盘被平均分成2个相等的扇形区域,分别标注数字1和2;B转盘被平均分成3个相等的扇形区域,分别标注数字-1,-2,-3.分别转动这两个转盘,将A盘所得结果记为x,B盘所得结果记为y,这样就确定了点P的坐标(x,y)
如图有两个可自由转动的转盘,A转盘被平均分成2个相等的扇形区域,分别标注数字1和2;B转盘被平均分成3个相等的扇形区域,分别标注数字-1,-2,-3.分别转动这两个转盘,将A盘所得结果记为x,B盘所得结果记为y,这样就确定了点P的坐标(x,y)