题目内容
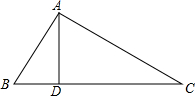 如图,在△ABC中,AB=13,AD=12,BD=5,AC=20,求△ABC的面积.
如图,在△ABC中,AB=13,AD=12,BD=5,AC=20,求△ABC的面积.考点:勾股定理
专题:
分析:先根据勾股定理的逆定理判断出△ABD的形状,进而可得出∠ADB=∠ADC=90°,由勾股定理求出CD的长,根据三角形的面积公式即可得出结论.
解答:解:在△ABD中,AB=13,AD=12,BD=5,
∵AD2+BD2=122+52=169,AB2=132=169,
∴AD2+BD2=AB2,
∴∠ADB=∠ADC=90°,
∴AD2+CD2=AC2.
∴CD2=202-122=256,
∵CD>0,
∴CD=16.
∴S△ABC=
×BC×AD=
×(5+16)×12=126.
∵AD2+BD2=122+52=169,AB2=132=169,
∴AD2+BD2=AB2,
∴∠ADB=∠ADC=90°,
∴AD2+CD2=AC2.
∴CD2=202-122=256,
∵CD>0,
∴CD=16.
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 由于大风,山坡上的一棵树甲被从点A处拦腰折断,如图所示,其树恰好落在另一棵树乙的根部C处,已知AB=4米,BC=13米,两棵树的株距(两棵树的水平距离)为12米,请你运用所学的知识求这棵树原来的高度.
由于大风,山坡上的一棵树甲被从点A处拦腰折断,如图所示,其树恰好落在另一棵树乙的根部C处,已知AB=4米,BC=13米,两棵树的株距(两棵树的水平距离)为12米,请你运用所学的知识求这棵树原来的高度.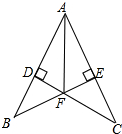 如图,BE⊥AC于点E,CD⊥AB于点D,BE、CD交于F,且AF平分∠BAC,求证:BF=FC.
如图,BE⊥AC于点E,CD⊥AB于点D,BE、CD交于F,且AF平分∠BAC,求证:BF=FC. 已知梯形ABCD中,AD∥BC,EF∥BC,AE=FC,EB=6
已知梯形ABCD中,AD∥BC,EF∥BC,AE=FC,EB=6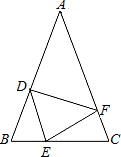 如图,在等腰三角形ABC中,AB=AC,BD=CE,BE=CF.
如图,在等腰三角形ABC中,AB=AC,BD=CE,BE=CF.