题目内容
解下列方程:
(1)x2+4x-1=0
(2)(x+4)2=5(x+4)
(1)x2+4x-1=0
(2)(x+4)2=5(x+4)
考点:解一元二次方程-因式分解法,解一元二次方程-配方法
专题:
分析:(1)利用配方法解答;
(2)移项后提公共因式即可.
(2)移项后提公共因式即可.
解答:(1)x2+4x-1=0
解:配方得,x2+4x+4=5,
(x+2)2=5,
解得,x+2=±
,
∴x1=-2+
,x2=-2-
;
(2)(x+4)2=5(x+4)
解:移项得,(x+4)2-5(x+4)=0,
提公因式得,(x+4)(x+4-5)=0,
∴x1=-4;x2=1.
解:配方得,x2+4x+4=5,
(x+2)2=5,
解得,x+2=±
| 5 |
∴x1=-2+
| 5 |
| 5 |
(2)(x+4)2=5(x+4)
解:移项得,(x+4)2-5(x+4)=0,
提公因式得,(x+4)(x+4-5)=0,
∴x1=-4;x2=1.
点评:本题考查了因式分解法和配方法解方程,要熟悉因式分解方可正确解答.

练习册系列答案
相关题目
满足下列条件的△ABC,不是直角三角形的是( )
| A、b2=a2-c2 |
| B、∠C=∠A-∠B |
| C、∠A:∠B:∠C=3:4:5 |
| D、a:b:c=12:13:5 |
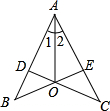 如图,CD⊥AB,BE⊥AC,垂足为D、E,BE、CD相交于O点,∠1=∠2,AB=AC,图中全等的三角形共有( )
如图,CD⊥AB,BE⊥AC,垂足为D、E,BE、CD相交于O点,∠1=∠2,AB=AC,图中全等的三角形共有( )| A、1对 | B、2对 | C、3对 | D、4对 |
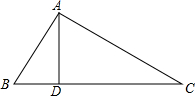 如图,在△ABC中,AB=13,AD=12,BD=5,AC=20,求△ABC的面积.
如图,在△ABC中,AB=13,AD=12,BD=5,AC=20,求△ABC的面积. 已知:如图,AB=AC,AE=AD.求证:∠AFE=∠AFD.
已知:如图,AB=AC,AE=AD.求证:∠AFE=∠AFD.