题目内容
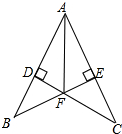 如图,BE⊥AC于点E,CD⊥AB于点D,BE、CD交于F,且AF平分∠BAC,求证:BF=FC.
如图,BE⊥AC于点E,CD⊥AB于点D,BE、CD交于F,且AF平分∠BAC,求证:BF=FC.考点:全等三角形的判定与性质
专题:证明题
分析:根据角平分线性质可得EF=DF,即可求得△BDF≌△CEF即可解题.
解答:解:∵AF平分∠BAC,
∴EF=DF,
∵在△BDF和△CEF中,
,
∴△BDF≌△CEF,(ASA)
∴BF=FC.
∴EF=DF,
∵在△BDF和△CEF中,
|
∴△BDF≌△CEF,(ASA)
∴BF=FC.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△BDF≌△CEF是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
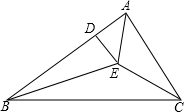 如图,E是△ABC内一点,EA、EB分别是∠BAC与∠ABC的平分线,且ED⊥AB于点D,连接EC,则∠AED+∠BEC的度数为( )
如图,E是△ABC内一点,EA、EB分别是∠BAC与∠ABC的平分线,且ED⊥AB于点D,连接EC,则∠AED+∠BEC的度数为( )| A、150° | B、165° |
| C、180° | D、195° |
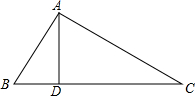 如图,在△ABC中,AB=13,AD=12,BD=5,AC=20,求△ABC的面积.
如图,在△ABC中,AB=13,AD=12,BD=5,AC=20,求△ABC的面积.