题目内容
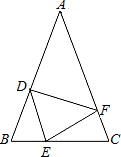 如图,在等腰三角形ABC中,AB=AC,BD=CE,BE=CF.
如图,在等腰三角形ABC中,AB=AC,BD=CE,BE=CF.(1)求证:△EBD≌△FCE;
(2)若∠A=40°,求∠DEF的度数.
考点:全等三角形的判定与性质
专题:
分析:(1)根据AB=AC可得∠B=∠C,即可求证△EBD≌△FCE;
(2)根据(1)中结论可以求得∠CEF=∠BDE即可解题.
(2)根据(1)中结论可以求得∠CEF=∠BDE即可解题.
解答:解:(1)∵AB=AC,
∴∠B=∠C,
在△EBD和△FCE中,
,
∴△EBD≌△FCE(SAS);
(2)∵△EBD≌△FCE,
∴∠CEF=∠BDE,
∵∠DEF=180°-∠BED-∠CEF,
∴∠DEF=180°-∠BED-∠BDE=∠B,
∵∠A=40°,AB=AC,
∴∠B=70°,
∴∠DEF=70°.
∴∠B=∠C,
在△EBD和△FCE中,
|
∴△EBD≌△FCE(SAS);
(2)∵△EBD≌△FCE,
∴∠CEF=∠BDE,
∵∠DEF=180°-∠BED-∠CEF,
∴∠DEF=180°-∠BED-∠BDE=∠B,
∵∠A=40°,AB=AC,
∴∠B=70°,
∴∠DEF=70°.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证△EBD≌△FCE是解题的关键.

练习册系列答案
相关题目
在下列实数中,无理数的个数为( )
-0.101001,
,
,
,-
,
,-
,0,-
.
-0.101001,
| 7 |
| 22 |
| 7 |
| 3 | 27 |
| π |
| 2 |
| 2 |
| 3 |
| 16 |
| A、1个 | B、2个 | C、3个 | D、4个 |
如图所示,对所给图形及说法正确的个数是( )


| A、0 | B、1 | C、2 | D、3 |
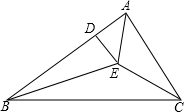 如图,E是△ABC内一点,EA、EB分别是∠BAC与∠ABC的平分线,且ED⊥AB于点D,连接EC,则∠AED+∠BEC的度数为( )
如图,E是△ABC内一点,EA、EB分别是∠BAC与∠ABC的平分线,且ED⊥AB于点D,连接EC,则∠AED+∠BEC的度数为( )| A、150° | B、165° |
| C、180° | D、195° |
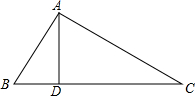 如图,在△ABC中,AB=13,AD=12,BD=5,AC=20,求△ABC的面积.
如图,在△ABC中,AB=13,AD=12,BD=5,AC=20,求△ABC的面积. 如图所示,⊙O是正方形ABCD的外接圆,过点A作圆的切线EF,那么∠EAB=
如图所示,⊙O是正方形ABCD的外接圆,过点A作圆的切线EF,那么∠EAB= 如图,在△ABC中,DE∥BC,AC=4,AB=3,EC=1,求AD,BD的长度.
如图,在△ABC中,DE∥BC,AC=4,AB=3,EC=1,求AD,BD的长度.