题目内容
 已知梯形ABCD中,AD∥BC,EF∥BC,AE=FC,EB=6
已知梯形ABCD中,AD∥BC,EF∥BC,AE=FC,EB=6| 3 |
| 4 |
| 1 |
| 3 |
考点:平行线分线段成比例
专题:计算题
分析:设AE=x,则FC=x,根据平行线分线段成比例定理得到
=
,然后解方程即可.
| x | ||
|
| ||
| x |
解答:解:设AE=x,则FC=x,
∵AD∥BC,EF∥BC,
∴AD∥EF∥BC,
∴
=
,即
=
,解得x=6,
即AE的长为6.
∵AD∥BC,EF∥BC,
∴AD∥EF∥BC,
∴
| AE |
| EB |
| DF |
| FC |
| x | ||
|
| ||
| x |
即AE的长为6.
点评:本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
下列qq的“表情图”中,属于轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
在下列实数中,无理数的个数为( )
-0.101001,
,
,
,-
,
,-
,0,-
.
-0.101001,
| 7 |
| 22 |
| 7 |
| 3 | 27 |
| π |
| 2 |
| 2 |
| 3 |
| 16 |
| A、1个 | B、2个 | C、3个 | D、4个 |
如图所示,对所给图形及说法正确的个数是( )


| A、0 | B、1 | C、2 | D、3 |
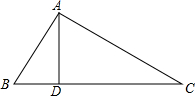 如图,在△ABC中,AB=13,AD=12,BD=5,AC=20,求△ABC的面积.
如图,在△ABC中,AB=13,AD=12,BD=5,AC=20,求△ABC的面积. 已知:如图,AB=AC,AE=AD.求证:∠AFE=∠AFD.
已知:如图,AB=AC,AE=AD.求证:∠AFE=∠AFD. 如图,在△ABC中,DE∥BC,AC=4,AB=3,EC=1,求AD,BD的长度.
如图,在△ABC中,DE∥BC,AC=4,AB=3,EC=1,求AD,BD的长度.