题目内容
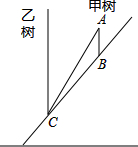 由于大风,山坡上的一棵树甲被从点A处拦腰折断,如图所示,其树恰好落在另一棵树乙的根部C处,已知AB=4米,BC=13米,两棵树的株距(两棵树的水平距离)为12米,请你运用所学的知识求这棵树原来的高度.
由于大风,山坡上的一棵树甲被从点A处拦腰折断,如图所示,其树恰好落在另一棵树乙的根部C处,已知AB=4米,BC=13米,两棵树的株距(两棵树的水平距离)为12米,请你运用所学的知识求这棵树原来的高度.考点:勾股定理的应用
专题:
分析:首先构造直角三角形,进而求出BD的长,进而求出AC的长,即可得出答案.
解答: 解:如图所示:延长AB,过点C作CD⊥AB延长线于点D,
解:如图所示:延长AB,过点C作CD⊥AB延长线于点D,
由题意可得:BC=13m,DC=12m,
故BD=
=5(m),
即AD=9m,
则AC=
=
=15(m),
故AC+AB=15+4=19(m),
答:树原来的高度19米.
 解:如图所示:延长AB,过点C作CD⊥AB延长线于点D,
解:如图所示:延长AB,过点C作CD⊥AB延长线于点D,由题意可得:BC=13m,DC=12m,
故BD=
| 132-122 |
即AD=9m,
则AC=
| AD2+CD2 |
| 92+122 |
故AC+AB=15+4=19(m),
答:树原来的高度19米.
点评:此题主要考查了勾股定理的应用,得出BD的长是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列qq的“表情图”中,属于轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
在下列实数中,无理数的个数为( )
-0.101001,
,
,
,-
,
,-
,0,-
.
-0.101001,
| 7 |
| 22 |
| 7 |
| 3 | 27 |
| π |
| 2 |
| 2 |
| 3 |
| 16 |
| A、1个 | B、2个 | C、3个 | D、4个 |
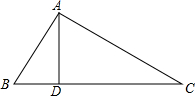 如图,在△ABC中,AB=13,AD=12,BD=5,AC=20,求△ABC的面积.
如图,在△ABC中,AB=13,AD=12,BD=5,AC=20,求△ABC的面积.