题目内容

6．已知点A（2，3）在直线y=2x+b上．则b的值为（　　）
A．-1B．0C．1D．2

分析 把点A（2，3）代入y=2x+b求出b的值即可．

解答 解：点A（2，3）代入直线y=2x+b
得：3=2×2+b，b=-1．
故选A．

点评 此题比较简单，解答此题的关键是熟知函数图象上点的坐标一定适合此函数的解析式．

练习册系列答案
相关题目
16．将（mx+3）（2-3x）展开后，结果不含x的一次项，则m的值为（　　）
A．0B．$\frac{9}{2}$C．-$\frac{9}{2}$D．$\frac{3}{2}$
17．当m≥-4时，一元二次方程x2-4x-m=0有实根；当-4≤m＜0时，两很同为正；当m＞0时，两根异号．
14．用配方法解下列方程：$\frac{1}{4}$x2-6x+3=0．
1．下列各数表示正确的是（　　）
A．5700000=57×106
B．0.0158（用四舍五入法精确到0.001）≈0.015
C．0.0000275=2.75×10-6
D．1.967（用四舍五入法精确到十分位）≈2.0
11．如图（1），在平面直角坐标系xOy中，直线y=2x-1与y轴相交于点A，与反比例函数y=$\frac{k}{x}$（x＞0）的图象相交于点B（m，2）．
（1）求反比例函数的表达式；
（2）若将直线y=2x-1向上平移4个单位长度后与y轴交于点C，求△ABC的面积；
（3）如图（2），将直线y=2x-1向上平移，与反比例函数的图象交于点D，连接DA，DB，若△ABD的面积为3，求平移后直线的表达式．
18．（1）问题背景
如图甲，∠ADC=∠B=90°，DE⊥AB，垂足为E，且AD=CD，DE=5，求四边形ABCD的面积．


小明发现四边形ABCD的一组领边AD=CD，这就为旋转作了铺垫．于是，小明同学有如下思考过程：
第一步：将△ADE绕点D逆时针旋转90°；
第二步：利用∠A与∠DCB互补，
证明F、C、B三点共线，
从而得到正方形DEBF；
进而求得四边形ABCD的面积．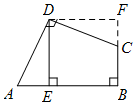
请直接写出四边形ABCD的面积为25．
（2）类比迁移
如图乙，P为等边△ABC外一点，BP=1，CP=3，且∠BPC=120°，求四边形ABPC的面积．
（3）拓展延伸
如图丙，在五边形ABCDE中，BC=4，CD+AB=4，AE=DE=6，AE⊥AB，DE⊥CD，求五边形ABCDE的面积．
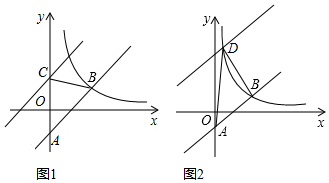
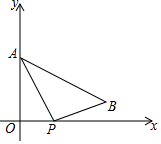15．如图，在平面直角坐标系中，点A（0，3）、点B（4，1），点P是x轴正半轴上一动点．给出4个结论：
①线段AB的长为5；
②在△APB中，若AP=$\sqrt{13}$，则△APB的面积是3$\sqrt{2}$；
③使△APB为等腰三角形的点P有3个；
④设点P的坐标为（x，0），则$\sqrt{9+{x}^{2}}$+$\sqrt{（4-x）^{2}+1}$的最小值为4$\sqrt{2}$．
其中正确的结论有④．
13．已知，正六边形ABCDEF在直角坐标系内的位置如图所示，点A的坐标为A（-1，0），点B在原点，把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转，每次翻转60°，经过2016次翻转之后，点B的经过的路径长是（2016$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网