题目内容
5.下列方程中,有实根的是( )| A. | $\sqrt{x+1}+\sqrt{x+2}+3=0$ | B. | $\sqrt{x-9}+\sqrt{4-x}=16$ | ||
| C. | $\sqrt{{x}^{2}+1}-\sqrt{{x}^{2}+2}=1-\frac{1}{\sqrt{{x}^{2}+1}}$ | D. | 6$\sqrt{{x}^{2}-2x+6}=21+2x-{x}^{2}$ |
分析 根据二次根式的非负性以及不等式的性质判断A、B、C无实数根,利用换元法解方程6$\sqrt{{x}^{2}-2x+6}$=21+2x-x2,判断D有实数根.
解答 解:A、∵$\sqrt{x+1}$≥0,$\sqrt{x+2}$≥0,
∴$\sqrt{x+1}$+$\sqrt{x+2}$+3≥3≠0,
所以方程$\sqrt{x+1}$+$\sqrt{x+2}$+3=0没有实数根,故本选项不符合题意;
B、由题意,得$\left\{\begin{array}{l}{x-9≥0}\\{4-x≥0}\end{array}\right.$,x无解,
所以方程$\sqrt{x-9}$+$\sqrt{4-x}$=16没有实数根,故本选项不符合题意;
C、∵x2+1<x2+2,
∴$\sqrt{{x}^{2}+1}$-$\sqrt{{x}^{2}+2}$<0,即方程左边为负数.
∵x2+1≥1,
∴$\frac{1}{\sqrt{{x}^{2}+1}}$≤1,
∴1-$\frac{1}{\sqrt{{x}^{2}+1}}$≥0,即方程右边为非负数,
所以方程$\sqrt{{x}^{2}+1}$-$\sqrt{{x}^{2}+2}$=1-$\frac{1}{\sqrt{{x}^{2}+1}}$没有实数根,故本选项不符合题意;
D、设$\sqrt{{x}^{2}-2x+6}$=y,则原方程可化为6y=27-y2,
解得y=3或y=-9(舍去).
当y=3时,x2-2x+6=9,
解得x=-1或3,
经检验,x=-1或3都是原方程的根,
所以方程6$\sqrt{{x}^{2}-2x+6}$=21+2x-x2有实数根,故本选项符合题意.
故选D.
点评 本题考查了无理方程,关键是掌握用换元法解无理方程.也考查了二次根式的非负性以及不等式的性质.

 出彩同步大试卷系列答案
出彩同步大试卷系列答案如图甲,∠ADC=∠B=90°,DE⊥AB,垂足为E,且AD=CD,DE=5,求四边形ABCD的面积.

小明发现四边形ABCD的一组领边AD=CD,这就为旋转作了铺垫.于是,小明同学有如下思考过程: 第一步:将△ADE绕点D逆时针旋转90°; 第二步:利用∠A与∠DCB互补, 证明F、C、B三点共线, 从而得到正方形DEBF; 进而求得四边形ABCD的面积. 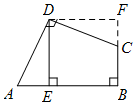 |
(2)类比迁移
如图乙,P为等边△ABC外一点,BP=1,CP=3,且∠BPC=120°,求四边形ABPC的面积.
(3)拓展延伸
如图丙,在五边形ABCDE中,BC=4,CD+AB=4,AE=DE=6,AE⊥AB,DE⊥CD,求五边形ABCDE的面积.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 63′ | B. | 10.5′ | C. | 103′ | D. | 105′ |
 已知,正六边形ABCDEF在直角坐标系内的位置如图所示,点A的坐标为A(-1,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2016次翻转之后,点B的经过的路径长是(2016$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
已知,正六边形ABCDEF在直角坐标系内的位置如图所示,点A的坐标为A(-1,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2016次翻转之后,点B的经过的路径长是(2016$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).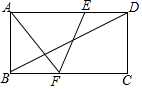 如图,在矩形ABCD中,点E、F分别是AD、BC上的点,连接AF、EF,EF与对角线BD交于点O.若AE=AF=CF=12,∠AEF=2∠ADB,则矩形ABCD的面积为108$\sqrt{3}$.
如图,在矩形ABCD中,点E、F分别是AD、BC上的点,连接AF、EF,EF与对角线BD交于点O.若AE=AF=CF=12,∠AEF=2∠ADB,则矩形ABCD的面积为108$\sqrt{3}$.