题目内容
14.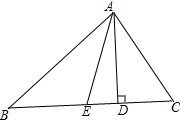 如图,AD、AE分别是△ABC的高、中线,AB=15,BC=14,CA=13.求:
如图,AD、AE分别是△ABC的高、中线,AB=15,BC=14,CA=13.求:(1)CD的长;
(2)AD的长;
(3)AE的长(精确到0.1)
分析 (1)设CD=x,则BD=14-x.在两个直角三角形中,根据勾股定理分别表示AD2,列方程求得x的值,再进一步求得CD的长;
(2)根据勾股定理即可得到结论;
(3)根据线段的中点的定义得到DE=2,然后根据勾股定理即可得到结论.
解答 解:(1)设CD=x,则BD=14-x.
根据勾股定理,得
AD2=AB2-BD2=AC2-CD2,
即225-(14-x)2=169-x2,
解得:x=5.
则CD=5,
(2)由(1)解得CD=5,
∵AC=13,
∴AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=12;
(3)∵AE分别是△ABC的中线,
∴CE=$\frac{1}{2}$BC=7,
∴DE=7-5=2,
∴AE=$\sqrt{D{E}^{2}+A{D}^{2}}$=$\sqrt{29}$.
点评 本题考查了勾股定理;熟练掌握勾股定理,由勾股定理得出方程求出AD是解决问题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
4.下列语句:
①相等的角是对顶角;
②如果两条直线被第三条直线所截,那么同位角相等;
③过直线外一点有且只有一条直线与已知直线平行;
④平行线间的距离处处相等.
其中正确的命题是( )
①相等的角是对顶角;
②如果两条直线被第三条直线所截,那么同位角相等;
③过直线外一点有且只有一条直线与已知直线平行;
④平行线间的距离处处相等.
其中正确的命题是( )
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
2.二元一次方程组$\left\{\begin{array}{l}{x+2y=2}\\{2x+y=-2}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=0}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$ |
6.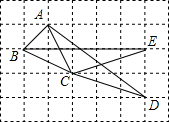 如图,在边长为1的小正方形组成的网格中,点A、B、C、D、E都在小正方形的顶点上.则tan∠ADC的值等于( )
如图,在边长为1的小正方形组成的网格中,点A、B、C、D、E都在小正方形的顶点上.则tan∠ADC的值等于( )
 如图,在边长为1的小正方形组成的网格中,点A、B、C、D、E都在小正方形的顶点上.则tan∠ADC的值等于( )
如图,在边长为1的小正方形组成的网格中,点A、B、C、D、E都在小正方形的顶点上.则tan∠ADC的值等于( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{10}}{10}$ |
 已知:如图,AM、CM平分∠BAD和∠BCD,若∠B=34°,∠D=42°,求∠M.
已知:如图,AM、CM平分∠BAD和∠BCD,若∠B=34°,∠D=42°,求∠M.