题目内容
5.若实数x,y满足(x-$\sqrt{{x}^{2}-2013}$)(y-$\sqrt{{y}^{2}-2013}$)=2013,则3x2-2y2+3x-3y-2012的值为1.分析 根据轮换对称式的性质得x=y,代入求出x,即可解决问题.
解答 解:∵(x-$\sqrt{{x}^{2}-2013}$)(y-$\sqrt{{y}^{2}-2013}$)=2013,
∴x、y是轮换对称式,
∴x=y,
∴x-$\sqrt{{x}^{2}-2013}$=±$\sqrt{2013}$,
解得x=±$\sqrt{2013}$,
∴原式=3x2-2x2+3x-3x-2012=x2-2012=1.
故答案为1.
点评 本题考查二次根式的化简、轮换对称式的性质,解题的关键是轮换对称式性质的应用,题目比较难,体现了转化的数学思想.

练习册系列答案
相关题目
14. 如图,在⊙O上有顶点C和动点P,位于直径AB的两侧,过点C作CP的垂线与PB的延长线交于点Q.已知⊙O的直径为10,tan∠ABC=$\frac{4}{3}$,则CQ最大值为( )
如图,在⊙O上有顶点C和动点P,位于直径AB的两侧,过点C作CP的垂线与PB的延长线交于点Q.已知⊙O的直径为10,tan∠ABC=$\frac{4}{3}$,则CQ最大值为( )
 如图,在⊙O上有顶点C和动点P,位于直径AB的两侧,过点C作CP的垂线与PB的延长线交于点Q.已知⊙O的直径为10,tan∠ABC=$\frac{4}{3}$,则CQ最大值为( )
如图,在⊙O上有顶点C和动点P,位于直径AB的两侧,过点C作CP的垂线与PB的延长线交于点Q.已知⊙O的直径为10,tan∠ABC=$\frac{4}{3}$,则CQ最大值为( )| A. | 5 | B. | $\frac{15}{2}$ | C. | $\frac{25}{4}$ | D. | $\frac{20}{3}$ |
15.在△ABC中,∠C=90°,AB的垂直平分线DE交AB于E,交BC于D,且CD:BD=1:2,BC=6cm,则D到AB的距离为多少( )
| A. | 1.5cm | B. | 2cm | C. | 3cm | D. | 4cm |
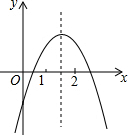 一次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论;
一次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论;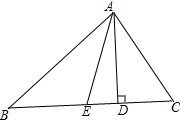 如图,AD、AE分别是△ABC的高、中线,AB=15,BC=14,CA=13.求:
如图,AD、AE分别是△ABC的高、中线,AB=15,BC=14,CA=13.求: