题目内容
9.已知$\frac{3{x}^{2}+4x-5}{{x}^{2}(x-2)}$=$\frac{A}{x}$+$\frac{B}{{x}^{2}}$+$\frac{C}{x-2}$(其中A,B,C均为常数),则A+B+C=$\frac{9}{2}$.分析 先根据分式的加减法则计算出等式右边的值,两边相比较即可得出结论.
解答 解:∵右边=$\frac{Ax(x-2)+B(x-2)+{cx}^{2}}{{x}^{2}(x-2)}$=$\frac{{Ax}^{2}-2Ax+Bx-2B+{cx}^{2}}{{x}^{2}(x-2)}$=$\frac{{(A+C)x}^{2}-(2A-B)x-2B}{{x}^{2}(x-2)}$,
∴$\left\{\begin{array}{l}A+C=2\\-2A+B=4\\ 2B=5\end{array}\right.$,解得$\left\{\begin{array}{l}A=\frac{11}{4}\\ B=\frac{5}{2}\\ C=-\frac{3}{4}\end{array}\right.$,
∴A+B+C=$\frac{11}{4}$+$\frac{5}{2}$-$\frac{3}{4}$=$\frac{9}{2}$.
故答案为:$\frac{9}{2}$.
点评 本题考查的是分式的加减法,熟知异分母的分式相加减的法则是解答此题的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
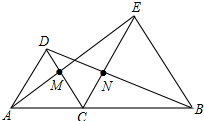 如图,A、C、B三点在同一条直线上,△DAC和△EBC都是等边三角形,AE、BD分别与CD、CE交于点M、N,求证:
如图,A、C、B三点在同一条直线上,△DAC和△EBC都是等边三角形,AE、BD分别与CD、CE交于点M、N,求证: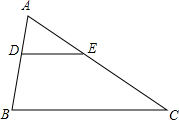 如图,点D,E分别在AB,AC上,DE∥BC,若AD:BD=2:3,BC=15cm,求DE的长.
如图,点D,E分别在AB,AC上,DE∥BC,若AD:BD=2:3,BC=15cm,求DE的长.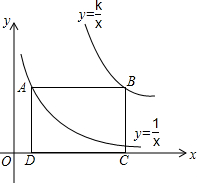 如图,点A在双曲线y=$\frac{1}{x}$上,点B在双曲线y=$\frac{k}{x}$上,且AB∥x轴,C,D两点在x轴上.若矩形ABCD的面积为6,求B点所在双曲线的函数表达式.
如图,点A在双曲线y=$\frac{1}{x}$上,点B在双曲线y=$\frac{k}{x}$上,且AB∥x轴,C,D两点在x轴上.若矩形ABCD的面积为6,求B点所在双曲线的函数表达式.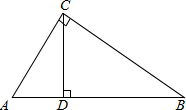 如图,在Rt△ABC中,CD是斜边AB上的高线,试猜想线段AC,AB,CD,BC是否对应成比例?如果对应成比例,请写出这个比例式,并进行验证;如果不能,请说明理由.
如图,在Rt△ABC中,CD是斜边AB上的高线,试猜想线段AC,AB,CD,BC是否对应成比例?如果对应成比例,请写出这个比例式,并进行验证;如果不能,请说明理由.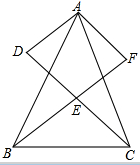 如图,△ADC≌△AFB,∠DAB=20°,DA∥BF,DC,BF交于点E.
如图,△ADC≌△AFB,∠DAB=20°,DA∥BF,DC,BF交于点E.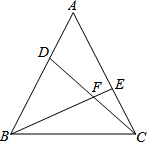 如图,已知D、E分别是等边△ABC中AB、AC上的点,且AE=BD,求∠BFC的度数.
如图,已知D、E分别是等边△ABC中AB、AC上的点,且AE=BD,求∠BFC的度数.