题目内容
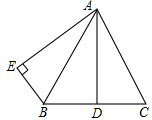 已知:如图,AB=AC,AD是BC边上的高,AB平分∠DAE,AE⊥BE,垂足为E.
已知:如图,AB=AC,AD是BC边上的高,AB平分∠DAE,AE⊥BE,垂足为E.(1)求证:BE=DC;
(2)当∠BAC=
考点:全等三角形的判定与性质,等腰三角形的性质
专题:
分析:(1)先证∠BAD=∠CAD,再证出∠BAE=∠BAD,得出∠BAE=∠CAD,即可证明△ABE≌△ACD,证出BE=DC;
(2)先证出∠BAC=∠ABC=∠C,得出△ABC是等边三角形,从而得出∠BAC=60°.
(2)先证出∠BAC=∠ABC=∠C,得出△ABC是等边三角形,从而得出∠BAC=60°.
解答:(1)证明:∵AB=AC,AD是BC边上的高,
∴∠BAD=∠CAD,∠ADC=90°,
∵AB平分∠DAE,
∴∠BAE=∠BAD,
∴∠BAE=∠CAD,
∵AE⊥BE,垂足为E,
∴∠AEB=90°,
∴∠AEB=∠ADC,
在△ABE和△ACD中,
∴△ABE≌△ACD(AAS),
∴BE=DC;
(2)60°;理由如下:
∵△ABE≌△ACD,
∴∠ABE=∠C,
∵AB∥AC,AB=AC,
∴∠ABE=∠BAC,∠ABC=∠C,
∴∠BAC=∠ABC=∠C,
∴△ABC是等边三角形,
∴∠BAC=60°;
故答案为:60.
∴∠BAD=∠CAD,∠ADC=90°,
∵AB平分∠DAE,
∴∠BAE=∠BAD,
∴∠BAE=∠CAD,
∵AE⊥BE,垂足为E,
∴∠AEB=90°,
∴∠AEB=∠ADC,
在△ABE和△ACD中,
|
∴△ABE≌△ACD(AAS),
∴BE=DC;
(2)60°;理由如下:
∵△ABE≌△ACD,
∴∠ABE=∠C,
∵AB∥AC,AB=AC,
∴∠ABE=∠BAC,∠ABC=∠C,
∴∠BAC=∠ABC=∠C,
∴△ABC是等边三角形,
∴∠BAC=60°;
故答案为:60.
点评:本题考查了等腰三角形的性质和全等三角形的判定与性质;证明三角形全等是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
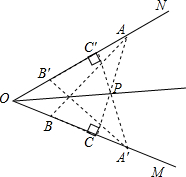 数学课上,探讨角平分线的作法时,小明发现只利用直角三角板也可以作角平分线,操作如下:
数学课上,探讨角平分线的作法时,小明发现只利用直角三角板也可以作角平分线,操作如下: 如图,已知CE、CF分别是△ABC中∠ACB及外角∠ACD的平分线,点E在AB上,EF交AC于点M,且EF∥BC.
如图,已知CE、CF分别是△ABC中∠ACB及外角∠ACD的平分线,点E在AB上,EF交AC于点M,且EF∥BC.
 已知:如图,二次函数的图象是由y=-x2向右平移1个单位,再向上平移4个单位所得到,这时图象与x轴的交点为A、B(A在B的左边),与y轴交于点C.
已知:如图,二次函数的图象是由y=-x2向右平移1个单位,再向上平移4个单位所得到,这时图象与x轴的交点为A、B(A在B的左边),与y轴交于点C. 将一个边长为1的正方形按如图所示的方法进行分割:部分①是整个正方形面积的一半,部分②是部分①面积的一半,部分③是部分②面积的一半,…,依此类推,通过计算此图形中部分①、部分②、部分③…的面积之和,可得到式子
将一个边长为1的正方形按如图所示的方法进行分割:部分①是整个正方形面积的一半,部分②是部分①面积的一半,部分③是部分②面积的一半,…,依此类推,通过计算此图形中部分①、部分②、部分③…的面积之和,可得到式子 如图,是一个长方形鸡场的平面示意图,一边靠墙,另外三面用篱笆围成.若篱笆总长为35m,所围的面积为150m2,求长方形鸡场的长和宽.
如图,是一个长方形鸡场的平面示意图,一边靠墙,另外三面用篱笆围成.若篱笆总长为35m,所围的面积为150m2,求长方形鸡场的长和宽. 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点D,过点D作EF∥BC交AB,AC于点E,F,若BE+CF=10,则EF=
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点D,过点D作EF∥BC交AB,AC于点E,F,若BE+CF=10,则EF=