题目内容
解方程:
(1)x2-x=5
(2)2(x+3)2=x(x+3)
(3)(x+4)(3x-2)+11=0
(4)x2+(2m+1)x+m2+m=0.
(1)x2-x=5
(2)2(x+3)2=x(x+3)
(3)(x+4)(3x-2)+11=0
(4)x2+(2m+1)x+m2+m=0.
考点:解一元二次方程-因式分解法,解一元二次方程-公式法
专题:
分析:(1)根据公式法,可得方程的解;
(2)根据因式分解法,可得方程的解;
(3)根据去括号、合并同类项,可化简方程,根据因式分解法,可得方程的解;
(4)根据因式分解法,可得方程的解.
(2)根据因式分解法,可得方程的解;
(3)根据去括号、合并同类项,可化简方程,根据因式分解法,可得方程的解;
(4)根据因式分解法,可得方程的解.
解答:解:(1)化为一般式,得x2-x-5=0,
a=1,b=-1,c=-5,△=b2-4ac=(-1)2-4×1×(-5)=21>0,
x=
,x1=
,x2=
;
(2)移项,得2(x+3)2-x(x-3)=0,
因式分解,得(x-3)(2x+6-x)=0,
x-3=0或x+6=0,
解得x1=3,x2=-6;
(3)化为一般式,得3x2+10x+3=0,
因式分解,得
(3x-1)(x-3)=0,
3x-1=0或x-3=0,
解得x1=
,x2=3;
(4)因式分解,得
(x+m+1)(x+m)=0,
x+m+1=0或x+m=0.
解得x1=-1-m,x2=-m.
a=1,b=-1,c=-5,△=b2-4ac=(-1)2-4×1×(-5)=21>0,
x=
-b±
| ||
| 2a |
1+
| ||
| 2 |
1-
| ||
| 2 |
(2)移项,得2(x+3)2-x(x-3)=0,
因式分解,得(x-3)(2x+6-x)=0,
x-3=0或x+6=0,
解得x1=3,x2=-6;
(3)化为一般式,得3x2+10x+3=0,
因式分解,得
(3x-1)(x-3)=0,
3x-1=0或x-3=0,
解得x1=
| 1 |
| 3 |
(4)因式分解,得
(x+m+1)(x+m)=0,
x+m+1=0或x+m=0.
解得x1=-1-m,x2=-m.
点评:本题考查了解一元二次方程,解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
用同样大小的黑色五角星按图所示的方式摆图案,按照这样的规律摆下去,第13个图案需要的黑色五角星的个数是( )


| A、18 | B、19 | C、21 | D、22 |
 如图,在△ABC中,AB=AC,AD是△ABC的中线,BE平分∠ABC交AD于点E,连接EC.求证:CE平分∠ACB.
如图,在△ABC中,AB=AC,AD是△ABC的中线,BE平分∠ABC交AD于点E,连接EC.求证:CE平分∠ACB.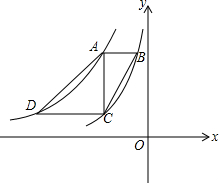 如图,双曲线y=-
如图,双曲线y=-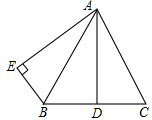 已知:如图,AB=AC,AD是BC边上的高,AB平分∠DAE,AE⊥BE,垂足为E.
已知:如图,AB=AC,AD是BC边上的高,AB平分∠DAE,AE⊥BE,垂足为E.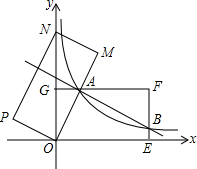 如图,在平面直角坐标系xOy中,矩形OEFG的顶点E的坐标为(4,0),顶点G的坐标为(0,2),将矩形OEFG绕点O逆时针旋转,使点F落在y轴的点N处,得到矩形OMNP,OM与GF交于点A.
如图,在平面直角坐标系xOy中,矩形OEFG的顶点E的坐标为(4,0),顶点G的坐标为(0,2),将矩形OEFG绕点O逆时针旋转,使点F落在y轴的点N处,得到矩形OMNP,OM与GF交于点A.