题目内容
 如图,已知CE、CF分别是△ABC中∠ACB及外角∠ACD的平分线,点E在AB上,EF交AC于点M,且EF∥BC.
如图,已知CE、CF分别是△ABC中∠ACB及外角∠ACD的平分线,点E在AB上,EF交AC于点M,且EF∥BC.(1)若∠B=45°,∠A=55°,求∠F的度数.
(2)求证:ME=MF.
考点:等腰三角形的判定与性质,平行线的性质
专题:
分析:(1)求出∠FCD=50°;由EF∥CD,得到∠F=∠FCD=50°.
(2)证明ME=MC;证明MF=MC,得到ME=MF.
(2)证明ME=MC;证明MF=MC,得到ME=MF.
解答: 解:(1)∵∠B=45°,∠A=55°,
解:(1)∵∠B=45°,∠A=55°,
∴∠ACD=∠A+∠B=100°;
∵CF平分∠ACD,
∴∠FCD=50°;而EF∥CD,
∴∠F=∠FCD=50°.
(2)∵CE平分∠ACB,
∴∠ACE=∠BCE;而EF∥BC,
∴∠MEC=∠BCE,
∴∠MEC=∠MCE,
∴ME=MC;同理可证MF=MC,
∴ME=MF.
 解:(1)∵∠B=45°,∠A=55°,
解:(1)∵∠B=45°,∠A=55°,∴∠ACD=∠A+∠B=100°;
∵CF平分∠ACD,
∴∠FCD=50°;而EF∥CD,
∴∠F=∠FCD=50°.
(2)∵CE平分∠ACB,
∴∠ACE=∠BCE;而EF∥BC,
∴∠MEC=∠BCE,
∴∠MEC=∠MCE,
∴ME=MC;同理可证MF=MC,
∴ME=MF.
点评:该题主要考查了平行线的性质、等腰三角形的判定及其性质等几何知识点及其应用问题;牢固掌握平行线的性质、等腰三角形的判定及其性质是解题的关键.

练习册系列答案
相关题目
 如图的平面展开图是( )
如图的平面展开图是( )A、 |
B、 |
C、 |
D、 |
 如图是在电脑屏幕上出现的长方形色块图,由6个颜色不同的正方形组成,设中间最小的一个正方形的边长为1,则正方形A的面积(阴影部分)是
如图是在电脑屏幕上出现的长方形色块图,由6个颜色不同的正方形组成,设中间最小的一个正方形的边长为1,则正方形A的面积(阴影部分)是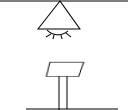 如图,正方形桌子的正上方挂着一盏灯,已知桌面连长为0.8m,桌面的高度为1m,灯泡距地面3m,求桌面在地面上的投影(正方形)面积.
如图,正方形桌子的正上方挂着一盏灯,已知桌面连长为0.8m,桌面的高度为1m,灯泡距地面3m,求桌面在地面上的投影(正方形)面积.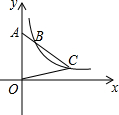 如图,点B、C在反比例函数y=
如图,点B、C在反比例函数y= 如图,在△ABC中,AB=AC,AD是△ABC的中线,BE平分∠ABC交AD于点E,连接EC.求证:CE平分∠ACB.
如图,在△ABC中,AB=AC,AD是△ABC的中线,BE平分∠ABC交AD于点E,连接EC.求证:CE平分∠ACB.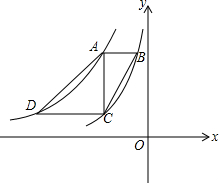 如图,双曲线y=-
如图,双曲线y=-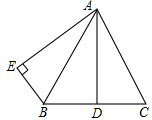 已知:如图,AB=AC,AD是BC边上的高,AB平分∠DAE,AE⊥BE,垂足为E.
已知:如图,AB=AC,AD是BC边上的高,AB平分∠DAE,AE⊥BE,垂足为E.