题目内容
 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点D,过点D作EF∥BC交AB,AC于点E,F,若BE+CF=10,则EF=
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点D,过点D作EF∥BC交AB,AC于点E,F,若BE+CF=10,则EF=考点:等腰三角形的判定与性质,平行线的性质
专题:
分析:先求出∠EBD=∠EDB,∠FDC=∠FCD,得出BE=DE,DF=CF,证出DE+DF=BE+CF=10.
解答:解:∵BD、CD分别平分∠ABC、∠ACB,
∴∠EBD=∠CBD,∠FCD=∠BCD,
∵EF∥BC,
∴∠EDB=∠CBD,∠FDC=∠BCD,
∴∠EBD=∠EDB,∠FDC=∠FCD,
∴BE=DE,DF=CF,
∴DE+DF=BE+CF=10.
∴∠EBD=∠CBD,∠FCD=∠BCD,
∵EF∥BC,
∴∠EDB=∠CBD,∠FDC=∠BCD,
∴∠EBD=∠EDB,∠FDC=∠FCD,
∴BE=DE,DF=CF,
∴DE+DF=BE+CF=10.
点评:本题考查了角平分线的定义、平行线的性质以及等腰三角形的判定;证明三角形是等腰三角形是解题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 如图的平面展开图是( )
如图的平面展开图是( )A、 |
B、 |
C、 |
D、 |
在平面直角坐标系中,将抛物线y=x2+1向右平移2个单位,再向下平移4个单位,得到的抛物线的解析式是( )
| A、y=(x+2)2-3 |
| B、y=(x-2)2-3 |
| C、y=(x-2)2+5 |
| D、y=(x+2)2+5 |
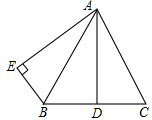 已知:如图,AB=AC,AD是BC边上的高,AB平分∠DAE,AE⊥BE,垂足为E.
已知:如图,AB=AC,AD是BC边上的高,AB平分∠DAE,AE⊥BE,垂足为E.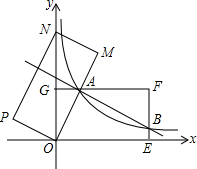 如图,在平面直角坐标系xOy中,矩形OEFG的顶点E的坐标为(4,0),顶点G的坐标为(0,2),将矩形OEFG绕点O逆时针旋转,使点F落在y轴的点N处,得到矩形OMNP,OM与GF交于点A.
如图,在平面直角坐标系xOy中,矩形OEFG的顶点E的坐标为(4,0),顶点G的坐标为(0,2),将矩形OEFG绕点O逆时针旋转,使点F落在y轴的点N处,得到矩形OMNP,OM与GF交于点A.
 如图,直线y=2x-2分别交x轴、y轴于B、A两点,交双曲线y=
如图,直线y=2x-2分别交x轴、y轴于B、A两点,交双曲线y= 如图,点A、E、F、C线上,AD∥BC,AD=CB,AE=CE,求证:∠B=∠D.
如图,点A、E、F、C线上,AD∥BC,AD=CB,AE=CE,求证:∠B=∠D.