题目内容
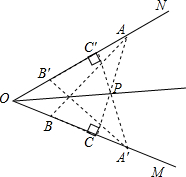 数学课上,探讨角平分线的作法时,小明发现只利用直角三角板也可以作角平分线,操作如下:
数学课上,探讨角平分线的作法时,小明发现只利用直角三角板也可以作角平分线,操作如下:①先让三角板的直角边BC落在OM上,使顶点A恰好落在ON上;
②按上述操作,再将该三角板放置到如图所示的△A′B′C′的位置,B′C′落在ON上,顶点A′落在OM上,AC与A′C′交于点P;
③作射线OP,则OP就是∠MON的平分线.
(1)小明在推证其作法正确性的过程中,仅得出△OAC≌△OA′C′,则这两个三角形全等的依据是
(2)在(1)的基础上,请你帮助小明继续完成证明过程.
考点:作图—基本作图,全等三角形的判定
专题:
分析:(1)在△OAC与△OA′C′中,满足∠AOC=∠A′OC,∠ACO=∠A′C′O=90°,AC=A′C′,根据AAS可得△OAC≌△OA′C′;
(2)由△OAC≌△OA′C′可得OC=OC′,再利用HL证明Rt△OCP≌△OC′P,那么∠COP=∠C′OP.
(2)由△OAC≌△OA′C′可得OC=OC′,再利用HL证明Rt△OCP≌△OC′P,那么∠COP=∠C′OP.
解答:证明:(1)在△OAC与△OA′C′中,
,
∴△OAC≌△OA′C′(AAS).
故答案为AAS;
(2)∵△OAC≌△OA′C′,
∴OC=OC′.
在Rt△OCP与△OC′P中,
,
∴Rt△OCP≌△OC′P(HL),
∴∠COP=∠C′OP,
即OP平分∠MON.
|
∴△OAC≌△OA′C′(AAS).
故答案为AAS;
(2)∵△OAC≌△OA′C′,
∴OC=OC′.
在Rt△OCP与△OC′P中,
|
∴Rt△OCP≌△OC′P(HL),
∴∠COP=∠C′OP,
即OP平分∠MON.
点评:本题考查了利用直角三角板作角平分线的方法,全等三角形的判定与性质,难度不大.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
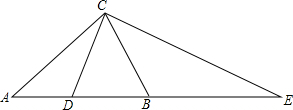 锐角△ABC中,AC=AB,CD是中线,延长AB到E使BE=AB,连接CE,此时△ACE为钝角三角形且∠DCB=36°,则∠DCE的度数是( )
锐角△ABC中,AC=AB,CD是中线,延长AB到E使BE=AB,连接CE,此时△ACE为钝角三角形且∠DCB=36°,则∠DCE的度数是( )| A、60° | B、72° |
| C、66° | D、不确定 |
 如图
如图 如图是在电脑屏幕上出现的长方形色块图,由6个颜色不同的正方形组成,设中间最小的一个正方形的边长为1,则正方形A的面积(阴影部分)是
如图是在电脑屏幕上出现的长方形色块图,由6个颜色不同的正方形组成,设中间最小的一个正方形的边长为1,则正方形A的面积(阴影部分)是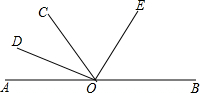 如图,已知A、O、B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC;
如图,已知A、O、B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC;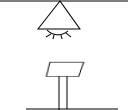 如图,正方形桌子的正上方挂着一盏灯,已知桌面连长为0.8m,桌面的高度为1m,灯泡距地面3m,求桌面在地面上的投影(正方形)面积.
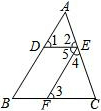
如图,正方形桌子的正上方挂着一盏灯,已知桌面连长为0.8m,桌面的高度为1m,灯泡距地面3m,求桌面在地面上的投影(正方形)面积.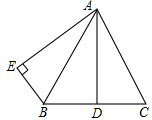 已知:如图,AB=AC,AD是BC边上的高,AB平分∠DAE,AE⊥BE,垂足为E.
已知:如图,AB=AC,AD是BC边上的高,AB平分∠DAE,AE⊥BE,垂足为E.