题目内容
14. 如图,有长为24米的篱笆,一面用墙(墙的最大可用长度a=15米)围成中间隔有一道篱笆的长方形花圃,设围成的花圃的面积为y 平方米,AB长为x米.
如图,有长为24米的篱笆,一面用墙(墙的最大可用长度a=15米)围成中间隔有一道篱笆的长方形花圃,设围成的花圃的面积为y 平方米,AB长为x米.(1)求y与x的函数关系式;
(2)并求出自变量x的取值范围;
(3)求围成的长方形花圃的最大面积及对应的AB的长.
分析 (1)根据AB为xm,BC就为(24-3x)m,利用长方形的面积公式,可求出关系式;
(2)根据墙的最大可用长度a=15米列不等式求出自变量x的取值范围;
(3)由(1)可知y和x为二次函数关系,根据二次函数的性质即可求围成的长方形花圃的最大面积及对应的AB的长;
解答 解:(1)y=x(24-3x)=-3x2+24x;
(2)∵0<24-3x≤15,
∴3≤x<8;
(3)y=-3x2+24x=-3(x-4)2+48,
∵3≤x<8;
∴当x=4时,y最大=48,即当AB=4米时,最大面积为48平方米.
点评 本题主要考查了二次函数的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出函数表达式,再根据二次函数性质解决问题.特别要注意垂直于墙的有三道篱笆.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
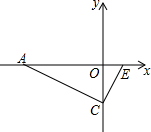 已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C(0,-2).如果BC=$\sqrt{5}$,∠ACB=90°.求这个二次函数解析式.
已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C(0,-2).如果BC=$\sqrt{5}$,∠ACB=90°.求这个二次函数解析式. 设有理数a,b在数轴上的对应点如图所示,化简|a+b|-|a|-|1-b|+|-b|.
设有理数a,b在数轴上的对应点如图所示,化简|a+b|-|a|-|1-b|+|-b|.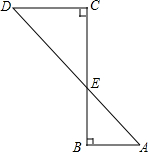 如图,∠A=θ,∠B=∠C=90°,AD与BC相交于点E,已知AD=m,AB=n,则CD等于mcosθ-n.
如图,∠A=θ,∠B=∠C=90°,AD与BC相交于点E,已知AD=m,AB=n,则CD等于mcosθ-n.