题目内容
18.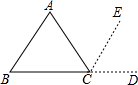 在下面空白处写出三角形内角的结论,已知和求证,并完成证明过程.
在下面空白处写出三角形内角的结论,已知和求证,并完成证明过程.(1)通过实验,用量角器多次测得任意一个三角形内角和大约为180度;
(2)根据(1)的事实,我们可以设法严格证明任意三角形内角和确为180度.
已知:CE∥AB
求证:∠A+∠B+∠ACB=180°
证明:
分析 (1)根据三角和定理:三角形的内角和是180度;
(2)根据平行线的性质证明三角形的内角和定理.
解答 解:(1)通过实验,用量角器多次测得任意一个三角形内角和大约为180度;
(2)根据(1)的事实,我们可以设法严格证明任意三角形内角和确为180度.
已知:CE∥AB,
求证:∠A+∠B+∠ACB=180°,
证明:∵CE∥AB,
∴∠ACE=∠A,∠ECD=∠B,
∵∠ACB+∠ACE+∠ECD=180°,
∴∠A+∠B+∠ACB=180°.
故答案为:180;180;CE∥AB;∠A+∠B+∠ACB=180°
点评 本题考查了三角形内角和定理,属于基础题,关键是掌握三角形内角和为180度.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
6.如果(ax-b)(x+2)=x2-4,那么( )
| A. | a=1,b=2 | B. | a=-1,b=-2 | C. | a=1,b=-2 | D. | a=-1,b=2 |
 如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1.
如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1.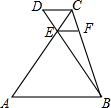 如图,AB∥CD∥EF,AC与BD相交于点E.
如图,AB∥CD∥EF,AC与BD相交于点E.