题目内容
13.若边长为a的等边三角形被平行于一边的直线分成等面积的两部分,则截得的梯形的上底长为$\frac{\sqrt{2}a}{2}$.分析 根据DE∥BC,证明△ADE∽△ABC,根据题意得到两个三角形的相似比,求出梯形的上底和下底.
解答  解:∵DE∥BC,
解:∵DE∥BC,
∴△ADE∽△ABC,
由题意得,△ADE的面积=△ABC的面积的一半,
∴$\frac{DE}{BC}=\sqrt{\frac{{S}_{△ADC}}{{S}_{△ABC}}}$=$\frac{\sqrt{2}}{2}$,又BC=a,
∴DE=$\frac{\sqrt{2}}{2}$a.
故答案为:$\frac{\sqrt{2}a}{2}$.
点评 本题考查的是相似三角形的判定和性质、等边三角形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在如图所示的方格中,填入1~9这9个数字,使每个“田”字形方格中的4个数字之和都相等,并且大方格两条对角线上的3个数字之和相等.
在如图所示的方格中,填入1~9这9个数字,使每个“田”字形方格中的4个数字之和都相等,并且大方格两条对角线上的3个数字之和相等. 在下面空白处写出三角形内角的结论,已知和求证,并完成证明过程.
在下面空白处写出三角形内角的结论,已知和求证,并完成证明过程.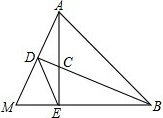 如图,AE、BD是△ABM的高,AE、BD交于点C,AE=BE,BD平分∠ABM.
如图,AE、BD是△ABM的高,AE、BD交于点C,AE=BE,BD平分∠ABM. 如图,在⊙O中,弦AB、CD相交于点E,∠BAC=40°,∠AED=75°,求∠ABD的度数.
如图,在⊙O中,弦AB、CD相交于点E,∠BAC=40°,∠AED=75°,求∠ABD的度数.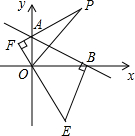 如图,直线y=-$\frac{1}{2}$x+2与坐标轴于A、B两点,BE⊥AB,BE=AB,AF⊥OE,垂足为F点
如图,直线y=-$\frac{1}{2}$x+2与坐标轴于A、B两点,BE⊥AB,BE=AB,AF⊥OE,垂足为F点