题目内容
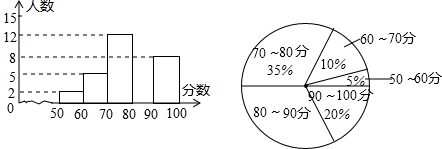
13.七年级(4)班与七年级(5)班每班的学生人数都为40,某次数学考试成绩统计,七年级(4)班给出了不完整的频数分布直方图如图1,七年级(5)班给出了不完整的扇形统计图如图2,这两个图,每组分数段的分数含左端点,不含右端点,已知本次考试两个班学生考试成绩都不低于50分,请根据图中提供的信息,完成下列问题:(1)七年级(4)班这次考试分数在80≤x<90分数段的同学有多少?并把七年级(4)班的频数分布直方图补充完整;
(2)两个班90分以上(含90分)的人数哪个班多?
(3)七年级(5)班分数在80≤x<90分数段的同学有多少?
分析 (1)观察频数分布直方图得到其他分数段的人数,根据考查人数是40人进行计算即可;
(2)通过直方图和扇形图得到两个班90分以上(含90分)的人数,比较即可;
(3)求出七年级(5)班分数在80≤x<90分数段的同学所占的百分比进行计算,得到答案.
解答 解:(1)七年级(4)班这次考试分数在80≤x<90分数段的同学有40-2-5-12-8=13人,
(2)七年级(4)班90分以上(含90分)的人数是8人,
七年级(5)班90分以上(含90分)的人数是40×20%=8人,
∴两个班90分以上(含90分)的人数一样多;
(3)七年级(5)班分数在80≤x<90分数段的同学所占的百分比是1-5%-10%-35%-20%=30%,
七年级(5)班分数在80≤x<90分数段的同学有40×30%=12人.
点评 本题考查的是频数分布直方图和扇形图,读懂频数分布直方图和扇形图,通过认真观察、分析、研究统计图正确获取信息是解题的关键.

练习册系列答案
相关题目
5.如图,图(1)是一个扇形AOB,将其作如下划分:第一次划分:如图(2)所示,得到扇形的总数为6个,分别为:扇形AOB、扇形AOC、扇形COB、扇形A1OB1、扇形A1OC1、扇形C1OB;第二次划分:如图(3)所示,在扇形C1OB1中,按上述划分方式继续划分,可以得到扇形的总数为11个;第三次划分:如图(4)所示;
依次划分下

(1)根据题意,完成表格
(2)请判断,按上述方式继续划分,能否得到扇形的总数为2000个?为什么?
依次划分下

(1)根据题意,完成表格
| 划分次数 | 扇形总个数 |
| 1 | 6 |
| 2 | 11 |
| 3 | 16 |
| 4 | 21 |
| … | … |
| n | 5n+1 |
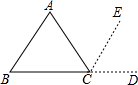 在下面空白处写出三角形内角的结论,已知和求证,并完成证明过程.
在下面空白处写出三角形内角的结论,已知和求证,并完成证明过程.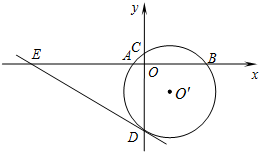 如图,已知⊙O′与x轴交于A、B两点,与y轴交于C、D两点,圆心O′的坐标是(1,-1),半径为$\sqrt{5}$.
如图,已知⊙O′与x轴交于A、B两点,与y轴交于C、D两点,圆心O′的坐标是(1,-1),半径为$\sqrt{5}$.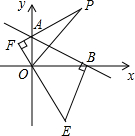 如图,直线y=-$\frac{1}{2}$x+2与坐标轴于A、B两点,BE⊥AB,BE=AB,AF⊥OE,垂足为F点
如图,直线y=-$\frac{1}{2}$x+2与坐标轴于A、B两点,BE⊥AB,BE=AB,AF⊥OE,垂足为F点