题目内容
2．已知a2-2a-2017=0，则a3-3a2-2015a-1=-2018．分析 由a2-2a-2017=0可变化为a2-2a=2017，将a3-3a2-2015a-1转化为a3-2a2-a2-2015a-1，再将a2-2a作为一个整体两次代入，即可求出该式的值．
解答 解：∵a2-2a-2017=0，即a2-2a=2017，
∴原式=a（a2-2a）-a2-2015a-1
=2017a-a2-2015a-1
=-（a2-2a）-1
=-2017-1
=-2018．
故答案为：-2018．
点评 本题考查因式分解的应用于代数式求值，解决本题的关键是将a2-2a作为一个整体代入，实现了降次，同时求出了代数式的值．
练习册系列答案
提分百分百检测卷系列答案
相关题目
13．已知Rt△ABC中，∠A=90°，∠B=30°，CD平分∠ACB且与AB边交于点D，AC=$\sqrt{6}$，则点D到边BC的距离是（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | $\sqrt{6}$ |
将n个边长都为2的正方形按如图所示摆放，点A1，A2，…，An分别是正方形的中心，则这n个正方形重叠部分的面积之和是n-1．
14．
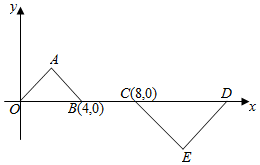如图所示，等腰直角三角形OAB和等腰直角三角形CDE是位似图形，点A的坐标为（2，2），点E的坐标为（12，-4），则这两个等腰直角三角形的位似中心的坐标为（$\frac{16}{3}$，0）．
如图所示，等腰直角三角形OAB和等腰直角三角形CDE是位似图形，点A的坐标为（2，2），点E的坐标为（12，-4），则这两个等腰直角三角形的位似中心的坐标为（$\frac{16}{3}$，0）． 
如图，矩形ABCD中，E为AB的中点．DF⊥CE．若AD=8．AB=4．则CF=$\frac{4\sqrt{17}}{17}$，DF=$\frac{16\sqrt{17}}{17}$．
12．当b＜0时，一次函数y=2x+b的图象经过（ ）
| A． | 第一、二、三象限 | B． | 第一、二、四象限 | C． | 第二、三、四象限 | D． | 第一、三、四象限 |