题目内容
20．（1）计算：（$\frac{1}{5}$x3y6-$\frac{9}{25}$x2y4）÷（-$\frac{3}{5}$xy2）2；（2）先化简，再求值：[（2x+y）（2x-y）-（x-2y）2-3x2]÷（2y），其中x=1，y=-2．
分析 （1）根据整式的除法可以解答本题；
（2）根据平方差公式、完全平方公式和整式的除法可以化简题目中的式子，然后将x、y的值代入即可解答本题．
解答 解：（1）（$\frac{1}{5}$x3y6-$\frac{9}{25}$x2y4）÷（-$\frac{3}{5}$xy2）2
=（$\frac{1}{5}$x3y6-$\frac{9}{25}$x2y4）÷（$\frac{9}{25}{x}^{2}{y}^{4}$）
=$\frac{5}{9}x{y}^{2}-1$；
（2）[（2x+y）（2x-y）-（x-2y）2-3x2]÷（2y）
=[4x2-y2-x2+4xy-4y2-3x2]÷（2y）
=（4xy-5y2）÷（2y）
=2x-2.5y，
当x=1，y=-2时，原式=2×1-2.5×（-2）=2+5=7．
点评 本题考查整式的混合运算-化简求值，解答本题的关键是明确整式的化简求值的方法．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
相关题目
10．某商场招聘员工一名，现有甲、乙两人竞聘，通过计算机、语言和商品知识三项测试，他们各自成绩（百分制）如下表所示
若商场需要招聘负责将商品拆装上架的人员，对计算机、语言和商品知识分别赋权2，3，5计算两名应试者的平均成绩，从他们的成绩看，应该录取谁？
| 应试者 | 计算机 | 语言 | 商品知识 |
| 甲 | 70 | 50 | 80 |
| 乙 | 90 | 75 | 45 |
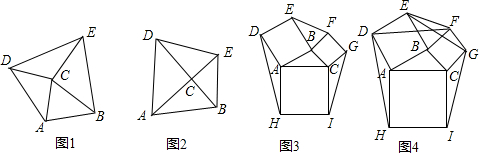
如图所示，所有四边形都是正方形，所有的三角形都是直角三角形，其中正方形D，C，A，B的面积分别为1，2，3，4，则正方形G的面积为10．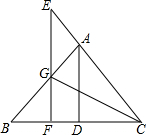
如图，△BAC与△EFC是两个完全相同的等腰直角三角形，其中∠BAC=∠EFC=90°，EF与AB相交于点G，D为BC的中点．
如图，木工师傅从边长为90cm的正三角形木板上锯出一正六边形木块，那么正六边形木板的边长为30．