题目内容
8.现代互联网技术的广泛应用,催生了快递行业的高速发展,小明计划给朋友快递一部分物品,经了解有甲乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.(1)根据题意,填写下表:
| 重量(千克) 费用(元) | 0.5 | 1 | 3 | 4 | … |
| 甲公司 | 11 | 22 | 52 | 67 | … |
| 乙公司 | 11 | 19 | 51 | 67 | … |
(3)小明应选择哪家快递公司更省钱?
分析 (1)根据甲、乙公司的收费方式,求出y值即可;
(2)根据甲、乙公司的收费方式结合数量关系,找出y甲、y乙(元)与x(千克)之间的函数关系式;
(3)分0<x≤1和x>1两种情况,分别求出y甲>y乙、y甲=y乙、y甲<y乙时x的取值范围,综上即可得出结论.
解答 解:(1)当x=0.5时,y甲=22×0.5=11;
当x=3时,y甲=22+15×2=52;
当x=1时,y乙=16×1+3=19;
当x=4时,y乙=16×4+3=67.
故答案为:11;52;19;67.
(2)当0<x≤1时,y甲=22x;
当x>1时,y甲=22+15(x-1)=15x+7.
∴y甲=$\left\{\begin{array}{l}{22x(0<x≤1)}\\{15x+7(x>1)}\end{array}\right.$.
y乙=16x+3(x>0).
(3)若0<x≤1,当y甲>y乙时,有22x>16x+3,
解得:x>$\frac{1}{2}$;
当y甲=y乙时,有22x=16x+3,
解得:x=$\frac{1}{2}$;
当y甲<y乙时,有22x<16x+3,
解得:x<$\frac{1}{2}$;
若x>1,当y甲>y乙时,有15x+7>16x+3,
解得:x<4;
当y甲=y乙时,有15x+7=16x+3,
解得:x=4;
当y甲<y乙时,有15x+7<16x+3,
解得:x>4.
综上可知:当快递物品少于$\frac{1}{2}$千克或多于4千克时,选择甲公司省钱;当快递物品等于$\frac{1}{2}$千克或等于4千克时,两家公司费用一样;当快递物品多于$\frac{1}{2}$千克而少于4千克时,选择乙公司省钱.
点评 本题考查了一次函数的应用,解题的关键是:(1)根据甲、乙公司的收费方式求出y值;(2)根据甲、乙公司的收费方式结合数量关系,找出y甲、y乙(元)与x(千克)之间的函数关系式;(3)分0<x≤1和x>1两种情况考虑y甲>y乙、y甲=y乙、y甲<y乙时x的取值范围.

 阅读快车系列答案
阅读快车系列答案(1)请借助以下记录确定y与x的函数关系式,并写出自变量x的取值范围;?
| x | 35 | 40 | 45 | 50 |
| y | 57 | 42 | 27 | 12 |
| 销售量P(件) | p=120-2x |
| 销售单价q(元/件) | 当1≤x<25时,q=x+60; 当25≤x≤50时,q=40+$\frac{1125}{x}$ |
(2)设该商品的利润为W(元),试求W与x的函数关系式;
(3)这50天,该超市哪一天获得的利润W(元)最大?最大利润是多少?
 “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为( )
“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为( )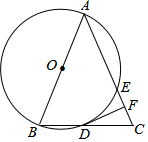 如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,过点D作DF⊥AC,垂足为点F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,过点D作DF⊥AC,垂足为点F.
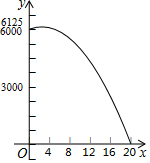 某商品的进价为每件40元,当售价为每件60元时,每星期可卖出300件,现需降价处理,且经市场调查,每降价1元,每星期可多卖出20件,在确保盈利的前提下,解答下列问题:
某商品的进价为每件40元,当售价为每件60元时,每星期可卖出300件,现需降价处理,且经市场调查,每降价1元,每星期可多卖出20件,在确保盈利的前提下,解答下列问题: