题目内容
5. 如图,在平面直角坐标系中,正比例函数y=3x与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,点A的横坐标为2,AC⊥x轴,垂足为C,连接BC.
如图,在平面直角坐标系中,正比例函数y=3x与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,点A的横坐标为2,AC⊥x轴,垂足为C,连接BC.(1)求反比例函数的表达式;
(2)求△ABC的面积;
(3)若点P是反比例函数y=$\frac{k}{x}$图象上的一点,△OPC与△ABC面积相等,请直接写出点P的坐标.
分析 (1)把A点横坐标代入正比例函数可求得A点坐标,代入反比例函数解析式可求得k,可求得反比例函数解析式;
(2)根据反比例函数的对称性得出点B的坐标,再利用三角形的面积公式解答即可;
(3)由条件可求得B、C的坐标,可先求得△ABC的面积,再结合△OPC与△ABC的面积相等求得P点坐标.
解答 解:(1)把x=2代入y=3x中,得y=2×3=6,
∴点A坐标为(2,6),
∵点A在反比例函数y=$\frac{k}{x}$的图象上,
∴k=2×6=12,
∴反比例函数的解析式为y=$\frac{12}{x}$;
(2)∵AC⊥OC,
∴OC=2,
∵A、B关于原点对称,
∴B点坐标为(-2,-6),
∴B到OC的距离为6,
∴S△ABC=2S△ACO=2×$\frac{1}{2}$×2×6=12,
(3)∵S△ABC=12,
∴S△OPC=12,
设P点坐标为(x,$\frac{12}{x}$),则P到OC的距离为|$\frac{12}{x}$|,
∴$\frac{1}{2}$×|$\frac{12}{x}$|×2=12,解得x=1或-1,
∴P点坐标为(1,12)或(-1,-12).
点评 本题主要考查待定系数法求函数解析式及函数的交点问题,在(1)中求得A点坐标、在(2)中求得P点到OC的距离是解题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
15.一元二次方程x2-3x+4=0根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 无实数根 | D. | 无法确定 |
20.下列说法不正确的是( )
| A. | “抛掷一枚硬币,硬币落地时正面朝上”是随机事件 | |
| B. | “任意打开数学教科书八年级下册,正好是第50页”是不可能事件 | |
| C. | “把4个球放入三个抽屉中,其中必有一个抽屉中至少有2个球”是必然事件 | |
| D. | “在一个不透明的袋子中,有5个除颜色外完全一样的小球,其中2个红球,3个白球,从中任意摸出1个小球,正好是红球”是随机事件 |
17.在平面直角坐标系中,点(1,7)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
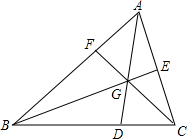 如图,在△ABC中,点D,E,F分别在三边上,E是AC的中点,AD,BE,CF交于一点G,BC=3DC,S△GEC=3,S△GBD=8,则△ABC的面积是30.
如图,在△ABC中,点D,E,F分别在三边上,E是AC的中点,AD,BE,CF交于一点G,BC=3DC,S△GEC=3,S△GBD=8,则△ABC的面积是30.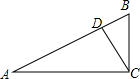 如图,在△ABC中,∠ACB=90°,D为AB边上一点,∠BCD=35°,∠BDC=80°.求∠A的度数.
如图,在△ABC中,∠ACB=90°,D为AB边上一点,∠BCD=35°,∠BDC=80°.求∠A的度数. 如图,把△ABC绕点C按逆时针方向旋转35°得到△A′B′C,A′B′交BC于点D,若∠A′DC=90°,则∠B=55°.
如图,把△ABC绕点C按逆时针方向旋转35°得到△A′B′C,A′B′交BC于点D,若∠A′DC=90°,则∠B=55°.