题目内容
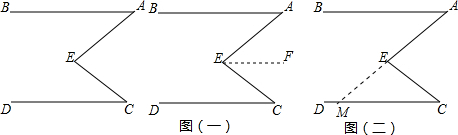
15.已知AB∥CD,图形中∠AEC与∠A、∠C有怎样的数量关系?并说明理由.请把以下推理过程补充完整:解法一:∠AEC=∠A+∠C
理由:如图(一),过点E作直线EFAB.
∵AB∥CD,EF∥AB
∴CD∥EF
∵AB∥EF,EF∥CD
∴∠A=∠AEF,∠C=∠CEF
∴∠AEC=∠AEF+∠CEF=∠A+∠C.
解法二:∠AEC=∠A+∠C
理由:如图(二),延长AE交CD于点M.
∵AB∥CD
∴∠A=∠AMC.
又∵∠AEC是三角形EMC的外角.
∴∠AEC=∠AMC+∠C.
∴∠AEC=∠A+∠C.
分析 解法一、求出CD∥EF,根据平行线的性质得出∠A=∠AEF,∠C=∠CEF,即可得出答案;
解法二、根据平行线的性质得出∠A=∠AMC,根据三角形的外角性质得出∠AEC=∠AMC+∠C,即可得出答案.
解答  解:∠AEC=∠A+∠C
解:∠AEC=∠A+∠C
理由:如图(一),过点E作直线EFAB,
∵AB∥CD,EF∥AB,
∴CD∥EF,
∵AB∥EF,EF∥CD,
∴∠A=∠AEF,∠C=∠CEF,
∴∠AEC=∠AEF+∠CEF=∠A+∠C;
解法二:∠AEC=∠A+∠C
理由:如图(二),延长AE交CD于点M.
∵AB∥CD
∴∠A=∠AMC,
∵∠AEC是△EMC的外角,
∴∠AEC=∠AMC+∠C,
∴∠AEC=∠A+∠C,
故答案为:CD,EF,A,AEF,C,CEF,A,AMC,EMC,AMC,C.
点评 本题考查了平行线的性质和三角形外角性质的应用,能正确作出辅助线是解此题的关键,注意:两直线平行,内错角相等.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
4.下列计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 3$\sqrt{5}$-$\sqrt{5}$=2 | C. | $\sqrt{6}$×$\sqrt{2}$=2$\sqrt{3}$ | D. | $\sqrt{6}$÷$\sqrt{2}$=3 |
 如图,在平面直角坐标系中,正比例函数y=3x与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,点A的横坐标为2,AC⊥x轴,垂足为C,连接BC.
如图,在平面直角坐标系中,正比例函数y=3x与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,点A的横坐标为2,AC⊥x轴,垂足为C,连接BC. 某中学新建了一栋4层的教学大楼,每层楼有8间教室,进出这栋大楼共有4道门,其中两道正门大小相同,两道侧门大小也相同.安全检查中,对4道门进行了测试:当同时开启一扇正门和两扇侧门,1分钟内可以通过280名学生;当同时开启一扇正门和一扇侧门时,4分钟内可通过800名学生.
某中学新建了一栋4层的教学大楼,每层楼有8间教室,进出这栋大楼共有4道门,其中两道正门大小相同,两道侧门大小也相同.安全检查中,对4道门进行了测试:当同时开启一扇正门和两扇侧门,1分钟内可以通过280名学生;当同时开启一扇正门和一扇侧门时,4分钟内可通过800名学生. 如图,将一张长方形纸片和一张直角三角形纸片叠放在一起,∠1+∠2的度数是270°.
如图,将一张长方形纸片和一张直角三角形纸片叠放在一起,∠1+∠2的度数是270°.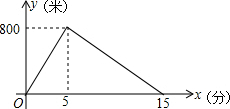 星期天早上,小明在锻炼身体,先从家跑步到公园,接着马上原路步行回家;如图是反映小明离家的路程y(米)与时间t(分)之间的函数关系的图象,则小明回家的速度是每分钟步行80米.
星期天早上,小明在锻炼身体,先从家跑步到公园,接着马上原路步行回家;如图是反映小明离家的路程y(米)与时间t(分)之间的函数关系的图象,则小明回家的速度是每分钟步行80米.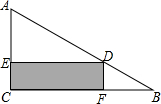 如图,在Rt△ABC的内部作一个矩形CEDF,其中CE、CF在三角形的边AC、BC上,已知AC=6cm,BC=8cm.设长方形的面积为y m2,边长DE=x m.
如图,在Rt△ABC的内部作一个矩形CEDF,其中CE、CF在三角形的边AC、BC上,已知AC=6cm,BC=8cm.设长方形的面积为y m2,边长DE=x m.