题目内容
如图,已知三角形ABC的底BC=1cm,面积为1cm2,A1,B1分别为AB,AC的中点,A2,B2分别为A1B,B1C的中点,以此类推:A4B4= ,S△AA4B4= .
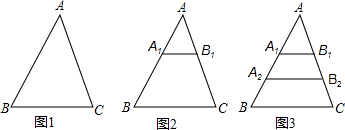

考点:相似三角形的判定与性质,三角形中位线定理,梯形中位线定理
专题:规律型
分析:根据三角形中位线定理求出A1B1=
BC=
cm,再根据梯形中位线定理可求出A4B4的长;根据相似三角形面积比等于相似比的平方即可求出S△AA4B4.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵A1,B1分别为AB,AC的中点,
∴A1B1是三角形ABC的中位线,
∴A1B1∥BC,A1B1=
BC=
cm.
∵A1B1∥BC,A2,B2分别为A1B,B1C的中点,
∴A2B2是梯形A1BCB1的中位线,
∴A2B2∥BC,A2B2=
(A1B1+BC)=
(
+1)=
cm,
同理,A3B3=
(A2B2+BC)=
(
+1)=
cm,
A4B4=
(A3B3+BC)=
(
+1)=
cm;
∵A4B4∥BC,
∴△AA4B4∽△ABC,
∴S△AA4B4:S△ABC=(A4B4:BC)2,
即S△AA4B4:1=(
:1)2=
,
∴S△AA4B4=
cm2.
故答案
cm;
cm2.
∴A1B1是三角形ABC的中位线,
∴A1B1∥BC,A1B1=
| 1 |
| 2 |
| 1 |
| 2 |
∵A1B1∥BC,A2,B2分别为A1B,B1C的中点,
∴A2B2是梯形A1BCB1的中位线,
∴A2B2∥BC,A2B2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
同理,A3B3=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 7 |
| 8 |
A4B4=
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 8 |
| 15 |
| 16 |
∵A4B4∥BC,
∴△AA4B4∽△ABC,
∴S△AA4B4:S△ABC=(A4B4:BC)2,
即S△AA4B4:1=(
| 15 |
| 16 |
| 225 |
| 256 |
∴S△AA4B4=
| 225 |
| 256 |
故答案
| 15 |
| 16 |
| 225 |
| 256 |
点评:本题考查了三角形中位线定理、梯形中位线定理和相似三角形的判定与性质,掌握相似三角形面积比等于相似比的平方是关键.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
抛物线y=2x2-3的顶点在( )
| A、x轴上 | B、y轴上 |
| C、第一象限 | D、第二象限 |
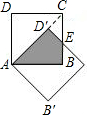 如图.边长为1的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转,则这两个正方形重叠部分的面积是( )
如图.边长为1的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转,则这两个正方形重叠部分的面积是( )A、
| ||
B、
| ||
C、
| ||
D、
|
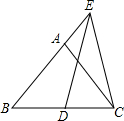 如图,在等边△ABC中,AB=8,E是BA延长线上一点,且EA=4,D是BC上一点,且ED=EC,则BD的长为( )
如图,在等边△ABC中,AB=8,E是BA延长线上一点,且EA=4,D是BC上一点,且ED=EC,则BD的长为( ) 一部分同学围在一起做“传数”游戏,我们把某同学传给后面的同学的数称为该同学的“传数”.游戏规则是:同学1心里先想好一个数,将这个数乘以2再加1后传给同学2,同学2把同学1告诉他的数除以2再减
一部分同学围在一起做“传数”游戏,我们把某同学传给后面的同学的数称为该同学的“传数”.游戏规则是:同学1心里先想好一个数,将这个数乘以2再加1后传给同学2,同学2把同学1告诉他的数除以2再减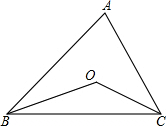 如图,点O是△ABC两内角平分线的交点
如图,点O是△ABC两内角平分线的交点