题目内容
 如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN.
如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN.(1)求证:BM=EN;
(2)若DN:CM=1:4,求
| MN |
| BM |
考点:翻折变换(折叠问题),全等三角形的判定与性质,勾股定理,菱形的判定与性质,矩形的判定与性质
专题:几何综合题
分析:(1)若要证明BM=EN,则可转化为证明△ABM≌△AEN即可;
(2)连接CN,过点N作NG⊥BC于G,由四边形ABCD是矩形,易得四边形CDNG是矩形,又由折叠的性质,可得四边形AMCN是菱形,由△CDN的面积与△CMN的面积比为1:4,根据等高三角形的面积比等于对应底的比,可得DN:CM=1:4,然后设DN=x,由勾股定理可求得MN的长,继而求得答案.
(2)连接CN,过点N作NG⊥BC于G,由四边形ABCD是矩形,易得四边形CDNG是矩形,又由折叠的性质,可得四边形AMCN是菱形,由△CDN的面积与△CMN的面积比为1:4,根据等高三角形的面积比等于对应底的比,可得DN:CM=1:4,然后设DN=x,由勾股定理可求得MN的长,继而求得答案.
解答:(1)证明:∵四边形ABCD是矩形,
∴AB=DC,∠B=∠BCD=90°,∠C=∠BAD=90°,
∵∠BAM+∠MAN=∠EAN+∠MAN=90°,
∴∠BAM=∠EAN,
∵将矩形ABCD折叠,使点C与点A重合,折痕为MN,
∴∠C=∠E=90°,
∴∠B=∠E=90°,
在△ABM和△AEN中,
,
∴△ABM≌△AEN(ASA),
∴BM=EN;
(2)连接CN,过点N作NG⊥BC于G,
∵四边形ABCD是矩形,
∴四边形CDNG是矩形,AD∥BC,
∴CD=NG,CG=DN,∠ANM=∠CMN,
由折叠的性质可得:AM=CM,∠AMN=∠CMN,
∴∠ANM=∠AMN,
∴AM=AN,
∴四边形AMCN是平行四边形,
∵AM=CM,
∴四边形AMCN是菱形,
∵△CDN的面积与△CMN的面积比为1:4,
∴DN:CM=1:4,
设DN=x,
则AN=AM=CM=CN=4x,AD=BC=5x,CG=x,
∴BM=x,GM=3x,
在Rt△CGN中,NG=
=
x,
在Rt△MNG中,MN=
=2
x,
∴
=2
.
∴AB=DC,∠B=∠BCD=90°,∠C=∠BAD=90°,
∵∠BAM+∠MAN=∠EAN+∠MAN=90°,
∴∠BAM=∠EAN,
∵将矩形ABCD折叠,使点C与点A重合,折痕为MN,
∴∠C=∠E=90°,
∴∠B=∠E=90°,

在△ABM和△AEN中,
|
∴△ABM≌△AEN(ASA),
∴BM=EN;
(2)连接CN,过点N作NG⊥BC于G,
∵四边形ABCD是矩形,
∴四边形CDNG是矩形,AD∥BC,
∴CD=NG,CG=DN,∠ANM=∠CMN,
由折叠的性质可得:AM=CM,∠AMN=∠CMN,
∴∠ANM=∠AMN,
∴AM=AN,
∴四边形AMCN是平行四边形,
∵AM=CM,
∴四边形AMCN是菱形,
∵△CDN的面积与△CMN的面积比为1:4,
∴DN:CM=1:4,
设DN=x,
则AN=AM=CM=CN=4x,AD=BC=5x,CG=x,
∴BM=x,GM=3x,
在Rt△CGN中,NG=
| CN2-CG2 |
| 15 |
在Rt△MNG中,MN=
| GM2+NG2 |
| 6 |
∴
| MN |
| BM |
| 6 |
点评:此题考查了折叠的性质、全等三角形的判定和性质、矩形的判定与性质、菱形的判定与性质以及勾股定理.此题难度较大,注意掌握辅助线的作法,注意折叠中的对应关系,注意数形结合与方程思想的应用.

练习册系列答案
相关题目
下列调查:①调查一批灯泡的使用寿命;②调查全班同学的身高;③调查市场上某食品的色素含量是否符合标准;④企业对招聘人员进行面试;⑤环保部门调查沱江某段水域的水质情况,采用抽样调查的方式;⑥旅客上飞机的安检.其中适宜用抽查的有( )
| A、2个 | B、3个 | C、4个 | D、5个 |
若将分式
中的x与y都扩大为原来的3倍,则分式的值( )
| x |
| x+y |
| A、扩大为原来的3倍 | ||
| B、不变 | ||
C、缩小为原来的
| ||
D、缩小为原来的
|




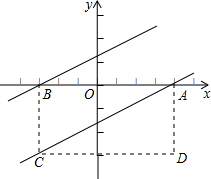 在平面直角坐标系中,矩形ABCD的边AB在x轴上,点A、B的横坐标分别为a+2与2a-5,且关于y轴对称,BC的长为3,且点C在第三象限.
在平面直角坐标系中,矩形ABCD的边AB在x轴上,点A、B的横坐标分别为a+2与2a-5,且关于y轴对称,BC的长为3,且点C在第三象限.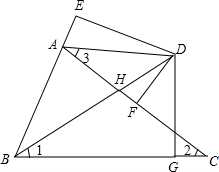 如图,在△ABC中,∠ABC的平分线BD交AC的中垂线DE于D,交AC于H,连接AD,DG⊥BC于G,交AC于K,延长BA至F,使AF=GC,连接DF.
如图,在△ABC中,∠ABC的平分线BD交AC的中垂线DE于D,交AC于H,连接AD,DG⊥BC于G,交AC于K,延长BA至F,使AF=GC,连接DF. 如图,已知四边形ABDE是平行四边形,C为边BD延长线上一点,连结AC、CE,使AB=AC.
如图,已知四边形ABDE是平行四边形,C为边BD延长线上一点,连结AC、CE,使AB=AC.
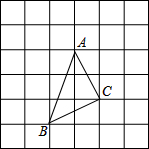 如图,在6×6的方格纸中有一个格点三角形ABC(三角形的顶点都在小正方形的顶点上),每个小正方形的边长都为1.
如图,在6×6的方格纸中有一个格点三角形ABC(三角形的顶点都在小正方形的顶点上),每个小正方形的边长都为1.