题目内容
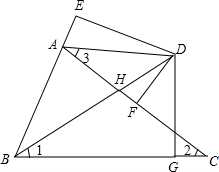 如图,在△ABC中,∠ABC的平分线BD交AC的中垂线DE于D,交AC于H,连接AD,DG⊥BC于G,交AC于K,延长BA至F,使AF=GC,连接DF.
如图,在△ABC中,∠ABC的平分线BD交AC的中垂线DE于D,交AC于H,连接AD,DG⊥BC于G,交AC于K,延长BA至F,使AF=GC,连接DF.(1)当∠1+2∠2=90°时,证明:DH=DK;
(2)当∠1=∠3时,证明:DF⊥AF.
考点:全等三角形的判定与性质,角平分线的性质,线段垂直平分线的性质
专题:证明题
分析:(1)根据余角的性质先求得∠DKE=∠GKC=90°-∠2,然后根据外角的性质求得∠DHE=∠1+∠2,再根据已知即可求得.
(2)根据线段的存在平分线的性质求得∠3=∠DCA,然后根据三角形的外角的性质和已知条件求得∠FAD=∠DCB,进而求得△AFD≌△CGD,根据全等三角形的性质即可求得∠AFD=∠DGC=90°
(2)根据线段的存在平分线的性质求得∠3=∠DCA,然后根据三角形的外角的性质和已知条件求得∠FAD=∠DCB,进而求得△AFD≌△CGD,根据全等三角形的性质即可求得∠AFD=∠DGC=90°
解答:证明:(1)∵∠1+2∠2=90°,
∴∠1+∠2=90°-∠2,
∵DG⊥BC,
∴∠DKE=∠GKC=90°-∠2,
∵∠DHE=∠1+∠2
∴∠DHE=∠DKE,
∴DH=DK;

(2)连接DC,
∵DE垂直平分AC,
∴DA=DC,∠3=∠DCA,
∵BD平分∠ABC,
∴∠ABC=2∠1,
∴∠FAD+∠3=2∠1+∠2,
∵∠1=∠3,
∴∠FAD=∠2+∠3,
∴∠DCB=∠2+∠DCA=∠2+∠3,
∴∠FAD=∠DCB,
在△AFD与△CGD中,
∴△AFD≌△CGD(SAS)
∴∠AFD=∠DGC,
∵∠DGC=90°,
∴∠AFD=90°,
∴DF⊥AF
∴∠1+∠2=90°-∠2,
∵DG⊥BC,
∴∠DKE=∠GKC=90°-∠2,
∵∠DHE=∠1+∠2
∴∠DHE=∠DKE,
∴DH=DK;

(2)连接DC,
∵DE垂直平分AC,
∴DA=DC,∠3=∠DCA,
∵BD平分∠ABC,
∴∠ABC=2∠1,
∴∠FAD+∠3=2∠1+∠2,
∵∠1=∠3,
∴∠FAD=∠2+∠3,
∴∠DCB=∠2+∠DCA=∠2+∠3,
∴∠FAD=∠DCB,
在△AFD与△CGD中,
|
∴△AFD≌△CGD(SAS)
∴∠AFD=∠DGC,
∵∠DGC=90°,
∴∠AFD=90°,
∴DF⊥AF
点评:此题考查了三角形外角的性质,三角形余角的性质,三角形全等的判定及性质,关键是根据题意做出辅助线,构造全等三角形,运用数形结合思想解答.

练习册系列答案
相关题目
 如图所示的圆锥主视图是一个等边三角形,边长为4cm,则这个圆锥的侧面积为( )
如图所示的圆锥主视图是一个等边三角形,边长为4cm,则这个圆锥的侧面积为( )| A、4πcm2 |
| B、16πcm2 |
| C、8πcm2 |
| D、12πcm2 |
 如图所示.∠1和∠2是一对( )
如图所示.∠1和∠2是一对( )| A、同位角 | B、同旁内角 |
| C、内错角 | D、对顶角 |
 如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN.
如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN.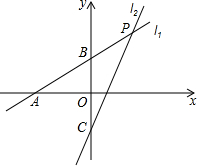 如图,直线l1:y=k1+b1(k≠0)分别与x轴、y轴相交于点A(-5,0)和点B(0,2),直线l2:y=2x+b2 与直线l1相交于点P、与y轴相交于点C,已知点P的纵坐标为3.
如图,直线l1:y=k1+b1(k≠0)分别与x轴、y轴相交于点A(-5,0)和点B(0,2),直线l2:y=2x+b2 与直线l1相交于点P、与y轴相交于点C,已知点P的纵坐标为3.