题目内容
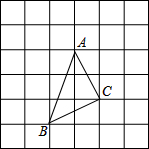如图，在6×6的方格纸中有一个格点三角形ABC（三角形的顶点都在小正方形的顶点上），每个小正方形的边长都为1．（1）建立直角坐标系，使A点的坐标是（2，-1），并写出B，C两点的坐标；
（2）判断△ABC的形状．
考点：勾股定理,坐标与图形性质,勾股定理的逆定理
专题：
分析：（1）找到x轴和y轴建立平面直角坐标系，从而写出B，C两点的坐标；
（2）根据勾股定理得到AB，BC，AC，再根据勾股定理的逆定理即可得到△ABC是等腰直角三角形．
（2）根据勾股定理得到AB，BC，AC，再根据勾股定理的逆定理即可得到△ABC是等腰直角三角形．
解答：解：（1）建立直角坐标系．
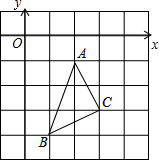
B点坐标为（1，-4），C点坐标为（3，-3）．
（2）由图知，AB=
=
，BC=
=
，AC=
=
，
则BC2+AC2=（
）2+（
）2=10，而AB2=（
）2=10．
所以AB2=BC2+AC2，且BC=AC．
故△ABC是等腰直角三角形．
B点坐标为（1，-4），C点坐标为（3，-3）．
（2）由图知，AB=
| 12+32 |
| 10 |
| 12+22 |
| 5 |
| 12+22 |
| 5 |
则BC2+AC2=（
| 5 |
| 5 |
| 10 |
所以AB2=BC2+AC2，且BC=AC．
故△ABC是等腰直角三角形．
点评：本题考查了坐标与图形性质，勾股定理和勾股定理的逆定理，熟练掌握网格结构准确找出对应点的位置是解题的关键．
练习册系列答案
相关题目
如图，在矩形ABCD中，AD＞AB，将矩形ABCD折叠，使点C与点A重合，折痕为MN．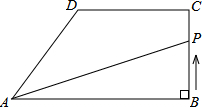
如图，在直角梯形ABCD中，AB∥DC，∠ABC=90°，AB=8cm．BC=4cm，CD=5cm．动点P从点B开始沿折线BC-CD-DA以1cm/s的速度运动到点A．设点P运动的时间为t（s），△PAB面积为S（cm2）．
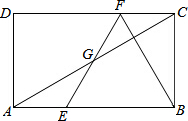如图，在矩形ABCD中，E、F分别是AB、CD上的点，AE=CF，连接EF、BF，EF交对角线AC于点G，若BE=BF，∠DFE=2∠BAC，BC=