题目内容
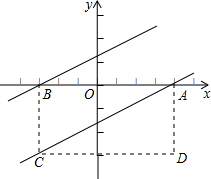 在平面直角坐标系中,矩形ABCD的边AB在x轴上,点A、B的横坐标分别为a+2与2a-5,且关于y轴对称,BC的长为3,且点C在第三象限.
在平面直角坐标系中,矩形ABCD的边AB在x轴上,点A、B的横坐标分别为a+2与2a-5,且关于y轴对称,BC的长为3,且点C在第三象限.(1)求顶点A、C的坐标;
(2)若y=kx+b是经过点B,且与AC平行的一条直线,试确定它的解析式.
考点:待定系数法求一次函数解析式,一次函数图象与几何变换
专题:计算题
分析:(1)根据关于y轴对称的点的坐标特征得到a+2+2a-5=0,解得a=1,则得到A点坐标为(3,0),B定坐标为(-3,0),然后利用矩形的性质和BC=3可得到C点坐标;
(2)先利用待定系数法确定直线AC的解析式为y=
x-
,然后利用一次函数图象与几何变换求解.
(2)先利用待定系数法确定直线AC的解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
解答:解:(1)∵点A与点B关于y轴对称,
∴a+2+2a-5=0,解得a=1,
∴A点坐标为(3,0),B定坐标为(-3,0),
∵矩形ABCD的边BC=3,
∴C点坐标为(-3,-3);
(2)设直线AC的解析式为y=mx+n,
把A(3,0)、(-3,-3)代入得
,
解得
,
∴直线AC的解析式为y=
x-
,
∵把直线y=
x-
向上平移3个单位得到过B点的直线,
∴经过点B,且与AC平行的直线解析式为y=
x-
+3=
x+
.
∴a+2+2a-5=0,解得a=1,
∴A点坐标为(3,0),B定坐标为(-3,0),
∵矩形ABCD的边BC=3,
∴C点坐标为(-3,-3);
(2)设直线AC的解析式为y=mx+n,
把A(3,0)、(-3,-3)代入得
|
解得
|
∴直线AC的解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
∵把直线y=
| 1 |
| 2 |
| 3 |
| 2 |
∴经过点B,且与AC平行的直线解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题考查了待定系数法求一次函数解析式:(1)先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;(2)将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;(3)解方程或方程组,求出待定系数的值,进而写出函数解析式.也考查了一次函数图象与几何变换.

练习册系列答案
相关题目
 已知a、b在数轴上对应点的位置如图,则下列结论中正确的是( )
已知a、b在数轴上对应点的位置如图,则下列结论中正确的是( )| A、|a|-b>0 |
| B、a-b>0 |
| C、a+b>0 |
| D、ab>0 |
用同样大小的黑色棋子按如图所示的规律摆放,那么2013个图形的黑色棋子有( )


| A、6041个 |
| B、6042个 |
| C、6142个 |
| D、6143个 |
 如图的几何体是由4个相同的小正方体组成.其左视图为( )
如图的几何体是由4个相同的小正方体组成.其左视图为( )A、 |
B、 |
C、 |
D、 |
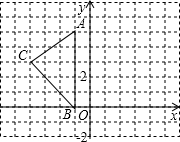 如图,在平面直角坐标系中,已知A(-1,5),B(-1,0),C(-4,3).
如图,在平面直角坐标系中,已知A(-1,5),B(-1,0),C(-4,3). 如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN.
如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN.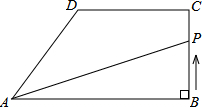 如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=8cm.BC=4cm,CD=5cm.动点P从点B开始沿折线BC-CD-DA以1cm/s的速度运动到点A.设点P运动的时间为t(s),△PAB面积为S(cm2).
如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=8cm.BC=4cm,CD=5cm.动点P从点B开始沿折线BC-CD-DA以1cm/s的速度运动到点A.设点P运动的时间为t(s),△PAB面积为S(cm2).