题目内容
14.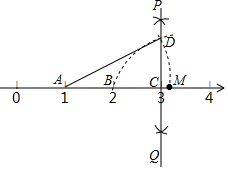 如图,数轴上点A、B、C分别对应1、2、3,过点C作PQ⊥AB,以点C为圆心,BC长为半径画弧,交PQ于点D,以点A为圆心,AD长为半径画弧,交数轴于点M,则点M对应的数是( )
如图,数轴上点A、B、C分别对应1、2、3,过点C作PQ⊥AB,以点C为圆心,BC长为半径画弧,交PQ于点D,以点A为圆心,AD长为半径画弧,交数轴于点M,则点M对应的数是( )| A. | $\sqrt{3}$+1 | B. | $\sqrt{5}$+1 | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
分析 根据数轴求出AC和CD,根据勾股定理求出AD=AM=$\sqrt{5}$,求出OM即可.
解答 解:根据数轴可知:AC=3-1=2,BC=CD=3-2=1,
由勾股定理得:AD=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
所以AM=AD=$\sqrt{5}$,
∵AO=1,
∴OM=1+$\sqrt{5}$,
故选B.
点评 本题考查了数轴和实数、勾股定理等知识点,能求出AD长是解此题的关键.

练习册系列答案
相关题目
9.已知二次函数y=ax2+bx+c(a>0)的图象过点(-2,0),(2,3),那么b的值为( )
| A. | -1 | B. | -$\frac{3}{4}$ | C. | 0 | D. | $\frac{3}{4}$ |
6.等腰三角形的一个外角为60°,则它的顶角的度数为( )
| A. | 120° | B. | 90° | C. | 60° | D. | 30° |
3. 如图,不能判定AB∥CD的是( )
如图,不能判定AB∥CD的是( )
 如图,不能判定AB∥CD的是( )
如图,不能判定AB∥CD的是( )| A. | ∠2=∠3 | B. | ∠1=∠4 | C. | ∠1=∠2 | D. | ∠1=∠3 |
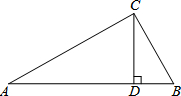 如图在△ABC中,CD是AB上的高且CD2=AD•BD,求证:△ABC是直角三角形.
如图在△ABC中,CD是AB上的高且CD2=AD•BD,求证:△ABC是直角三角形. 高考英语听力测试期间,需要杜绝考点周围的噪音,如图,点A是某市一高考考点,在位于A考点南偏西15°方向距离125米的C处有一消防队,在听力考试期间,消防队突然接到报警电话,告知在位于C点北偏东75°方向的F点处突发火灾,消防队必须立即赶往救火.已知消防车的警报声传播半径为100米,若消防车的警报声对听力测试造成影响,则消防车必须改进行驶,试问:消防车是否需要改道行驶?请说明理由.
高考英语听力测试期间,需要杜绝考点周围的噪音,如图,点A是某市一高考考点,在位于A考点南偏西15°方向距离125米的C处有一消防队,在听力考试期间,消防队突然接到报警电话,告知在位于C点北偏东75°方向的F点处突发火灾,消防队必须立即赶往救火.已知消防车的警报声传播半径为100米,若消防车的警报声对听力测试造成影响,则消防车必须改进行驶,试问:消防车是否需要改道行驶?请说明理由.