题目内容
9.已知二次函数y=ax2+bx+c(a>0)的图象过点(-2,0),(2,3),那么b的值为( )| A. | -1 | B. | -$\frac{3}{4}$ | C. | 0 | D. | $\frac{3}{4}$ |
分析 将点(-2,0),(2,3)代入y=ax2+bx+c后,将两方程相减消去a、c即可得.
解答 解:将点(-2,0),(2,3)代入y=ax2+bx+c,
得:$\left\{\begin{array}{l}{4a-2b+c=0}&{①}\\{4a+2b+c=3}&{②}\end{array}\right.$,
②-①,得:4b=3,
解得:b=$\frac{3}{4}$,
故选:D.
点评 本题主要考查二次函数图象上点的坐标特征,掌握函数图象上的点的坐标满足函数解析式是解题的关键.

练习册系列答案
相关题目
18.数学兴趣小组的小颖想测量教学楼前的一棵树的高度,下午课外活动时她测得一根长为1米的竹竿的影长是0.8米,测树高时,这棵树在地面上影长为2.6米,请计算树高为( )米.
| A. | 3.25 | B. | 4.25 | C. | 4.45 | D. | 4.75 |
14.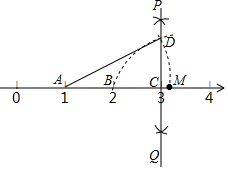 如图,数轴上点A、B、C分别对应1、2、3,过点C作PQ⊥AB,以点C为圆心,BC长为半径画弧,交PQ于点D,以点A为圆心,AD长为半径画弧,交数轴于点M,则点M对应的数是( )
如图,数轴上点A、B、C分别对应1、2、3,过点C作PQ⊥AB,以点C为圆心,BC长为半径画弧,交PQ于点D,以点A为圆心,AD长为半径画弧,交数轴于点M,则点M对应的数是( )
 如图,数轴上点A、B、C分别对应1、2、3,过点C作PQ⊥AB,以点C为圆心,BC长为半径画弧,交PQ于点D,以点A为圆心,AD长为半径画弧,交数轴于点M,则点M对应的数是( )
如图,数轴上点A、B、C分别对应1、2、3,过点C作PQ⊥AB,以点C为圆心,BC长为半径画弧,交PQ于点D,以点A为圆心,AD长为半径画弧,交数轴于点M,则点M对应的数是( )| A. | $\sqrt{3}$+1 | B. | $\sqrt{5}$+1 | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
1.民兴中学某班教室有50人在开家长会,其中有3名老师,12名家长,35名学生.校长在门外听到有人在发言,
那么发言人是老师或学生的概率为( )
那么发言人是老师或学生的概率为( )
| A. | $\frac{19}{25}$ | B. | $\frac{3}{10}$ | C. | $\frac{47}{50}$ | D. | $\frac{1}{2}$ |
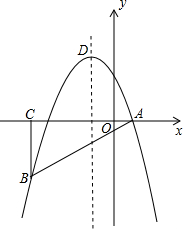 如图,在平面直角坐标系中,△ABC为等腰直角三角形,∠ACB=90°,抛物线y=-x2+bx+c经过A,B两点,其中点A,C的坐标分别为(1,0),(-4,0),抛物线的顶点为点D.
如图,在平面直角坐标系中,△ABC为等腰直角三角形,∠ACB=90°,抛物线y=-x2+bx+c经过A,B两点,其中点A,C的坐标分别为(1,0),(-4,0),抛物线的顶点为点D. 在边长为1的小正方形网格中,△AOB的顶点均在格上,且坐标分别为A(1,2),B(3,1),O(0,0)
在边长为1的小正方形网格中,△AOB的顶点均在格上,且坐标分别为A(1,2),B(3,1),O(0,0) 有理数a、b在数轴上的对应点位置如图所示,请化简:
有理数a、b在数轴上的对应点位置如图所示,请化简: