题目内容
2. 高考英语听力测试期间,需要杜绝考点周围的噪音,如图,点A是某市一高考考点,在位于A考点南偏西15°方向距离125米的C处有一消防队,在听力考试期间,消防队突然接到报警电话,告知在位于C点北偏东75°方向的F点处突发火灾,消防队必须立即赶往救火.已知消防车的警报声传播半径为100米,若消防车的警报声对听力测试造成影响,则消防车必须改进行驶,试问:消防车是否需要改道行驶?请说明理由.
高考英语听力测试期间,需要杜绝考点周围的噪音,如图,点A是某市一高考考点,在位于A考点南偏西15°方向距离125米的C处有一消防队,在听力考试期间,消防队突然接到报警电话,告知在位于C点北偏东75°方向的F点处突发火灾,消防队必须立即赶往救火.已知消防车的警报声传播半径为100米,若消防车的警报声对听力测试造成影响,则消防车必须改进行驶,试问:消防车是否需要改道行驶?请说明理由.
分析 首先过点A作AH⊥CF于点H,易得∠ACH=60°,然后利用三角函数的知识,求得AH的长,继而可得消防车是否需要改进行驶.
解答  解:如图:过点A作AH⊥CF于点H,
解:如图:过点A作AH⊥CF于点H,
由题意得:∠MCF=75°,∠CAN=15°,AC=125米,
∵CM∥AN,
∴∠ACM=∠CAN=15°,
∴∠ACH=∠MCF-∠ACM=75°-15°=60°,
∴在Rt△ACH中,AH=AC•sin∠ACH=125×$\frac{\sqrt{3}}{2}$≈108.25(米)>100米.
答:消防车不需要改道行驶.
点评 此题考查了解直角三角形的应用-方向角问题.此题难度适中,注意能借助于方向角构造直角三角形,并利用解直角三角形的知识求解是解此题的关键.

练习册系列答案
相关题目
14.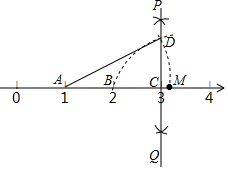 如图,数轴上点A、B、C分别对应1、2、3,过点C作PQ⊥AB,以点C为圆心,BC长为半径画弧,交PQ于点D,以点A为圆心,AD长为半径画弧,交数轴于点M,则点M对应的数是( )
如图,数轴上点A、B、C分别对应1、2、3,过点C作PQ⊥AB,以点C为圆心,BC长为半径画弧,交PQ于点D,以点A为圆心,AD长为半径画弧,交数轴于点M,则点M对应的数是( )
 如图,数轴上点A、B、C分别对应1、2、3,过点C作PQ⊥AB,以点C为圆心,BC长为半径画弧,交PQ于点D,以点A为圆心,AD长为半径画弧,交数轴于点M,则点M对应的数是( )
如图,数轴上点A、B、C分别对应1、2、3,过点C作PQ⊥AB,以点C为圆心,BC长为半径画弧,交PQ于点D,以点A为圆心,AD长为半径画弧,交数轴于点M,则点M对应的数是( )| A. | $\sqrt{3}$+1 | B. | $\sqrt{5}$+1 | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
 小明调查了班级里20名同学本学期计划购买课外书的花费情况,并将结果绘制成了扇形统计图.
小明调查了班级里20名同学本学期计划购买课外书的花费情况,并将结果绘制成了扇形统计图. 在边长为1的小正方形网格中,△AOB的顶点均在格上,且坐标分别为A(1,2),B(3,1),O(0,0)
在边长为1的小正方形网格中,△AOB的顶点均在格上,且坐标分别为A(1,2),B(3,1),O(0,0)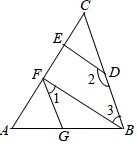 如图,DE⊥AC,∠AGF=ABC,∠1+∠2=180°,
如图,DE⊥AC,∠AGF=ABC,∠1+∠2=180°, 如图,已知∠1+∠2=180°,∠B=∠3,试判断∠BAC和∠CED的大小关系,并说明理由.
如图,已知∠1+∠2=180°,∠B=∠3,试判断∠BAC和∠CED的大小关系,并说明理由.