题目内容
7.有四张背面一模一样的卡片,卡片正面分别写着一个函数关系式,分别是y=2x,y=x2-3(x>0),y=$\frac{2}{x}$(x>0),y=-$\frac{1}{3x}$(x<0),将卡片顺序打乱后,随意从中抽取一张,取出的卡片上的函数是y随x的增大而增大的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
分析 利用正比例函数、二次函数以及反比例函数的性质可判断函数y=2x,y=x2-3(x>0),y=-$\frac{1}{3x}$(x<0),是y随x的增大而增大,然后根据概率公式可求出取出的卡片上的函数是y随x的增大而增大的概率.
解答 解:函数y=2x,y=x2-3(x>0),y=$\frac{2}{x}$(x>0),y=-$\frac{1}{3x}$(x<0)中,有y=2x,y=x2-3(x>0),y=-$\frac{1}{3x}$(x<0),是y随x的增大而增大,
所以随意从中抽取一张,取出的卡片上的函数是y随x的增大而增大的概率是$\frac{3}{4}$.
故选C.
点评 本题考查了概率公式:随机事件A的概率P(A)=事件A可能出现的结果数除以所有可能出现的结果数.也考查了正比例函数、二次函数以及反比例函数的性质.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
2.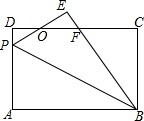 如图,已知长方形ABCD中,AD=6,AB=8,P是AD边上的点,将△ABP沿BP折叠,使点A落在点E上,PE、BE与CD分别交于点O、F,且OD=OE,则AP的长为( )
如图,已知长方形ABCD中,AD=6,AB=8,P是AD边上的点,将△ABP沿BP折叠,使点A落在点E上,PE、BE与CD分别交于点O、F,且OD=OE,则AP的长为( )
 如图,已知长方形ABCD中,AD=6,AB=8,P是AD边上的点,将△ABP沿BP折叠,使点A落在点E上,PE、BE与CD分别交于点O、F,且OD=OE,则AP的长为( )
如图,已知长方形ABCD中,AD=6,AB=8,P是AD边上的点,将△ABP沿BP折叠,使点A落在点E上,PE、BE与CD分别交于点O、F,且OD=OE,则AP的长为( )| A. | 4.8 | B. | 5 | C. | 5.2 | D. | 5.4 |
17.若两个相似三角形的周长比为1:3,则面积比为( )
| A. | 1:3 | B. | 3:1 | C. | 1:9 | D. | 9:1 |
 A、B两城相距600千米,一辆客车从A城开往B城,车速为每小时80千米,同时一辆出租车从B城开往A城,车速为毎小时100千米,设客车出时间为t.
A、B两城相距600千米,一辆客车从A城开往B城,车速为每小时80千米,同时一辆出租车从B城开往A城,车速为毎小时100千米,设客车出时间为t.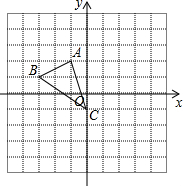 已知△ABC在坐标系中的位置如图:
已知△ABC在坐标系中的位置如图: 如图,∠ABC=∠DCB=90°,且AC=BD.AB与DC相等吗?∠BAC与∠CDB相等吗?为什么?
如图,∠ABC=∠DCB=90°,且AC=BD.AB与DC相等吗?∠BAC与∠CDB相等吗?为什么? 如图,在平面直角坐标系xOy中,A(-1,5),B(-2,0),C(-4,3).
如图,在平面直角坐标系xOy中,A(-1,5),B(-2,0),C(-4,3).