题目内容
16. 如图,在平面直角坐标系xOy中,A(-1,5),B(-2,0),C(-4,3).
如图,在平面直角坐标系xOy中,A(-1,5),B(-2,0),C(-4,3).(1)请画出△ABC关于y轴对称的△A'B′C′(其中A'、B′、C′分别是A、B、C的对称点,不写画法);
(2)写出C′的坐标,并求△ABC的面积;
(3)在y轴上找出点P的位置,使线段PA+PB的最小.
分析 (1)首先确定A、B、C三点关于y轴对称的对称点位置,然后再连接即可;
(2)根据平面直角坐标系可得C′的坐标,利用矩形的面积减去周围多余三角形的面积可得△ABC的面积;
(3)A与A′关于y轴对称,连接AB,与y轴交点就是P的位置.
解答 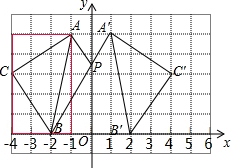 解:(1)如图所示:
解:(1)如图所示:
(2)C′的坐标(4,3),
△ABC的面积:3×5-$\frac{1}{2}$×2×3-$\frac{1}{2}$×2×3-$\frac{1}{2}$×1×5=15-3-3-2.5=6.5;
(3)连接A′B,与y轴的交点就是P的位置.
点评 此题主要考查了作图--轴对称变换,以及最短路线,关键是几何图形都可看做是由点组成,我们在画一个图形的轴对称图形时,也就是确定一些特殊点的对称点.在直线L上的同侧有两个点A、B,在直线L上有到A、B的距离之和最短的点存在,可以通过轴对称来确定,即作出其中一点关于直线L的对称点,对称点与另一点的连线与直线L的交点就是所要找的点.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
7.有四张背面一模一样的卡片,卡片正面分别写着一个函数关系式,分别是y=2x,y=x2-3(x>0),y=$\frac{2}{x}$(x>0),y=-$\frac{1}{3x}$(x<0),将卡片顺序打乱后,随意从中抽取一张,取出的卡片上的函数是y随x的增大而增大的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
11.已知一个三角形的两边长分别是4和10,那么它的第三边长可能是下列值中的( )
| A. | 5 | B. | 6 | C. | 11 | D. | 16 |
 如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB,若BE=2cm,试求出AE的长度.
如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB,若BE=2cm,试求出AE的长度.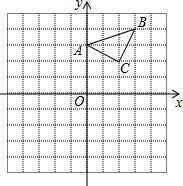 已知:在平面直角坐标系中,△ABC三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
已知:在平面直角坐标系中,△ABC三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)